Lecture 9

Summary

Fields and conductors
Electric potential
Point charges

Written Quiz Ch. 23

Electric potential

distributed charge example

Example #1

conductors

Example #2

Review concentric shells example Serway PSE6 24.51
A hollow conducting sphere is surrounded by a larger concentric spherical conducting shell.
The inner sphere has charge −Q, and the outer shell has net charge +3Q.
The charges are in electrostatic equilibrium. (a) Using Gauss' law, find the charges and the
electric fields everywhere. (b) Find the electric potential everywhere, assuming V = 0 at r = ∞.

Review Knight2 problem 29.65

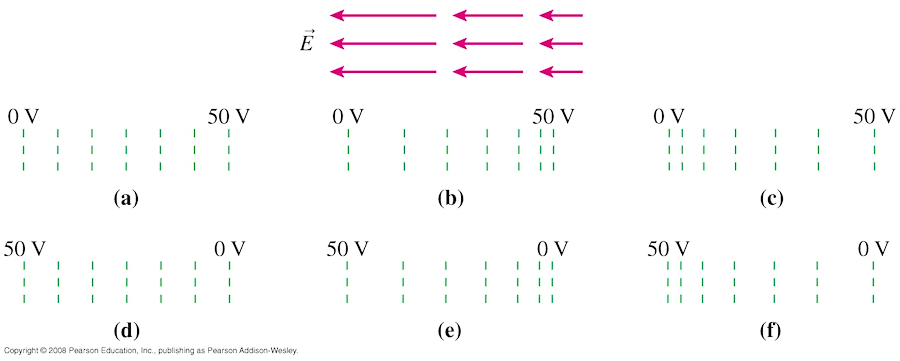
The figure at right shows two uniformly charged spheres. What is the potential difference between points a and b? Which point is at the higher potential? Hint: The potential at any point is the superposition of the potentials due to all charges.
(compare with conducting spheres)

E and V
- E points "downhill" on the V "surface"
- E is perpendicular to equipotential lines
- E is the slope of the electric potential function
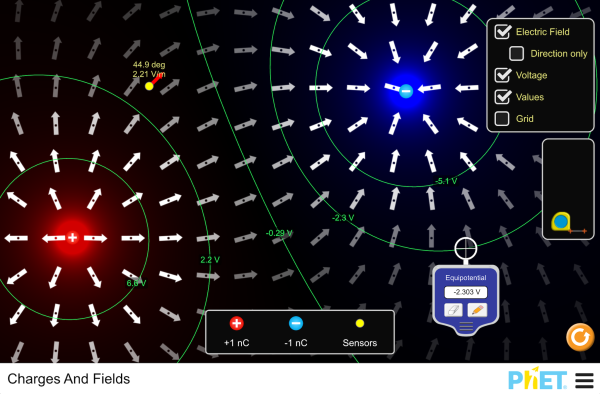
- 2-D fields and potential applet:
End of material on Exam I
Exam I

Bring a calculator (no mobile devices allowed) and your prepared 8-½×11 reference sheet
6 true/false questions (12 pts)
6 multiple-choice questions (18 pts)
3 free-response questions, each with multiple parts (70 pts)

Prepare:
Read textbook sections 25-1 and 25-2 before the next lecture

POP4 20.25a
A rod of length L has a nonuniform charge density λ = αx, where α is a positive constant. What are the units of α? Serway POP4 20.P.25

A. C/m
B. C/m²
C. C/m³
D. C²/N·m²
Answer

POP4 20.28
How many electrons should be removed from a 0.300-m-radius metal sphere to produce a 7.50-kV potential at the surface?
A. 5.38×10⁸
B. 2.24×10¹⁰
C. 1.56×10¹²
D. 8.77×10¹⁴
Answer

Knight2 stt 30.3
Which set of equipotential surfaces matches this electric field?
Knight2 Stop to Think 30.3

Answer

Walker5e 20.48a
Walker5e figure 20-36

Equipotential lines for a system are shown in the figure above. In which direction does the electric field point?
four possible directions

Answer

Walker5e 20.89
Walker5e figure 20-36

Notice in the figure above that the electric potential increases by 10.0 V as one moves 0.040 m in the positive x direction, and increases by 10.0 V as one moves 0.020 m in the positive y direction. Find the x- and y-components of the field to find the magnitude of E.
A. 559 V/m
B. 500 V/m
C. 250 V/m
D. 10 V/m
Answer

B. C/m²

The units of λ must be C/m, and because the units of x are meters, the units of α must be C/m², so that
λ = αx = (C/m²)×(m) = C/m.

C. 1.56×10¹²

The best answer is (c). The electric field points "downhill" on the potential surface, so that rules out (d), (e), and (f). The magnitude of the electric field is the slope of the potential surface, so the equipotential lines should be more closely spaced where the field is strongest. That rules out (a) and (b).

four possible directions

C.
The field points "downhill" on the potential surface, perpendicular to the equipotential lines, hence it must point down and to the left, in direction C.

Walker5e figure 20-36 field components

A. 559 V/m