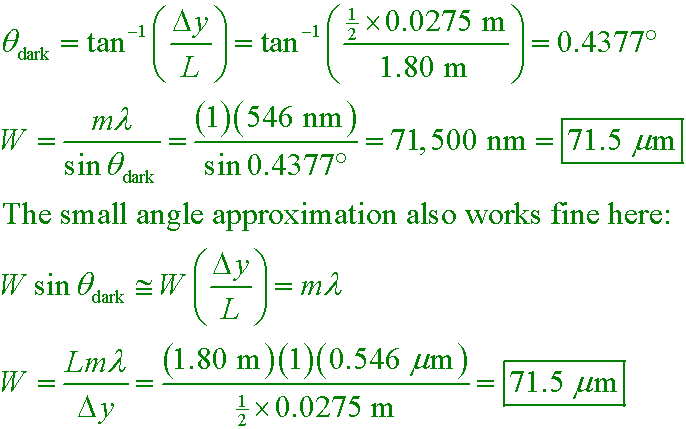Summary
- Magnifying glass
- Young's interference
- Thin film interference
- Written Quiz Ch. 27

- Diffraction
- Lecture learning outcomes
A student who masters the topics in this lecture will be able to:
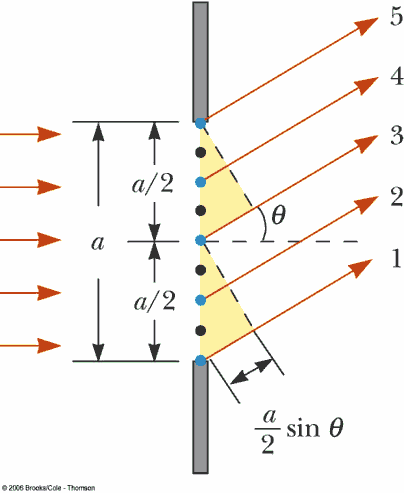
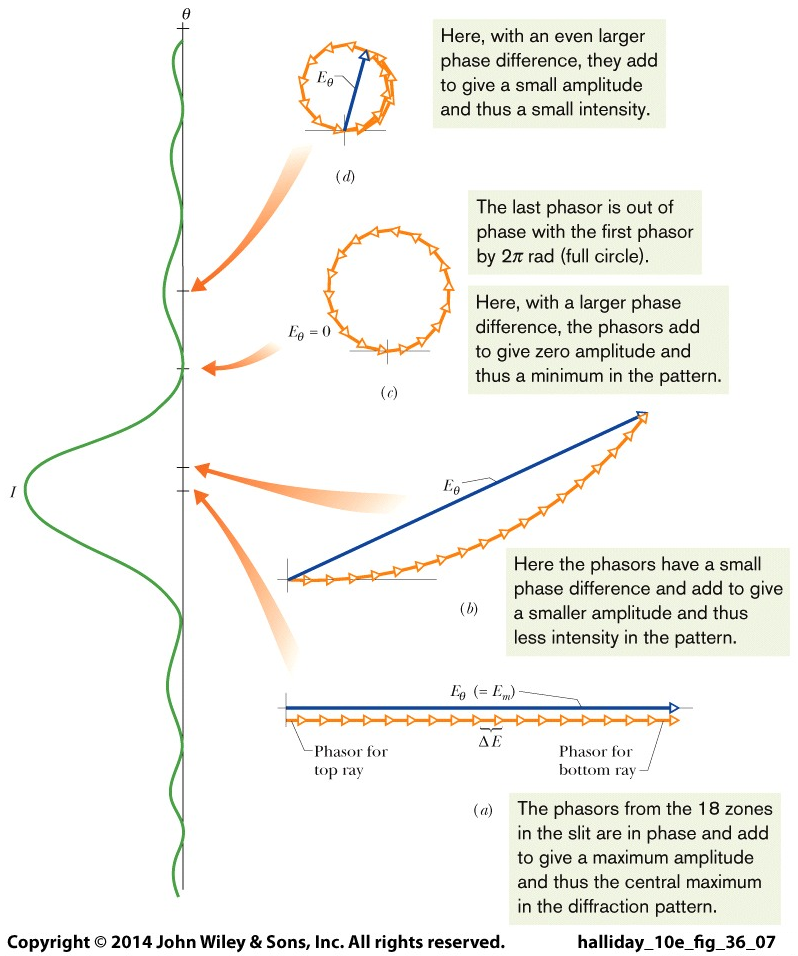
- describe the phenomenon of diffraction in terms wave interaction with an aperture or obstacle.
- use algebra to find the aperture width W, angle to a dark fringe θdark, order number m, or wavelength λ for single-slit diffraction when any three of these quantities are given
Practice:
Try these additional examples
Example #3
Example #4
Prepare:
Read textbook section 28-5 before the next lecture
gc6 24.q17
Blue light is shined through a single slit to produce a diffraction pattern on a screen. What will happen to the
pattern if red light is used instead?
A. The pattern will not change.
B. The pattern will condense.
C. The pattern will expand.
D. The pattern will be too dim to see.
Answer
gc6 24.24mod
When light of λ = 415 nm falls on a single slit that is 18.0 µm wide, how wide is the central bright fringe on a screen 2.55 m away?
 A. 588 µm
A. 588 µm
B. 85.0 mm
C. 11.8 cm
D. 2.64 m
Answer
Walker5e 28.CnEx.10
If the width of the slit through which light passes is reduced, the central bright fringe will _____.
A. become wider
B. become narrower
C. remain the same size
Answer
Walker5e 28.46
Green light (λ = 546 nm) strikes a single slit at normal incidence. What width slit will produce a central maximum that is 2.75 cm wide on a screen 1.80 m from the slit?
 A. 35.7 µm
A. 35.7 µm
B. 71.5 µm
C. 143 µm
D. 546 µm
Answer
C. The pattern will expand.
Red light has a longer wavelength than blue, and the separation between adjacent maxima in the diffraction pattern is linearly dependent upon the wavelength.
C. 11.8 cm

A. become wider
A narrower slit causes the light waves to spread out more because the slit becomes more like a point source of light. Mathematically, the right side of the equation m λ will remain constant, so a decrease in W forces an increase in θdark.
B. 71.5 µm
The angle can be found from geometry, keeping in mind it measures the angle between the center of central bright fringe to its edge, so use half the width of the central maximum in your calculation.
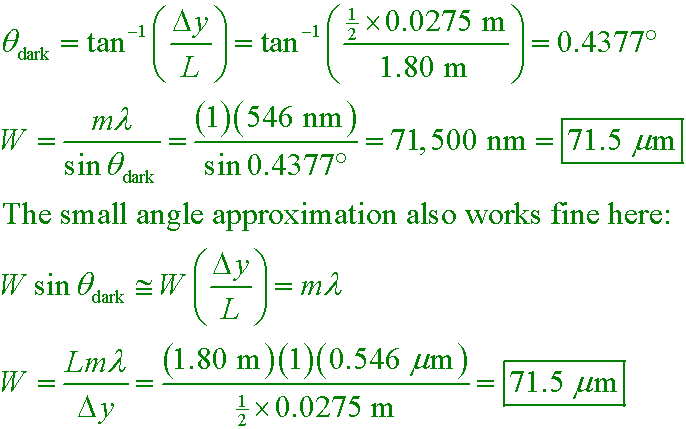



 A. 588 µm
A. 588 µm