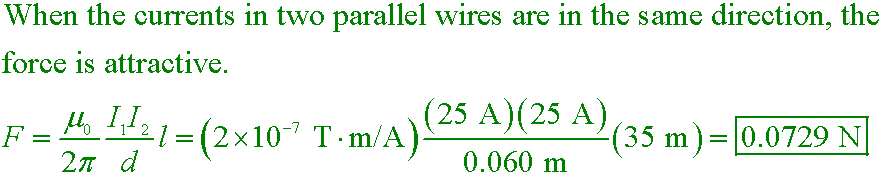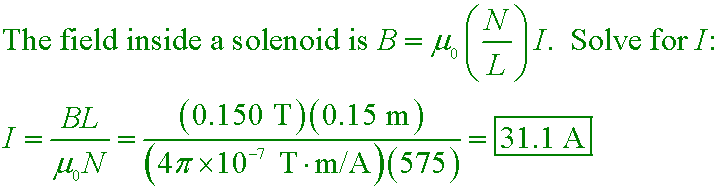Summary

• Currents produce magnetic fields
• Fields exert forces on currents
• Charged particles in a magnetic field

  



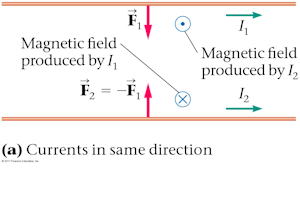
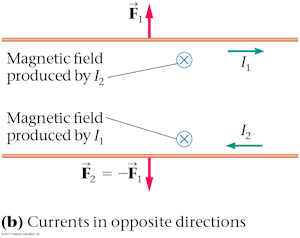
• Force between parallel wires applet

Example #1


• Parallel currents video



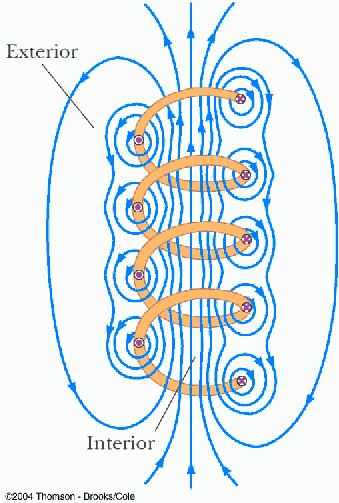
• Solenoids

Example #2





• Lecture learning outcomes
  A student who masters the topics in this lecture will be able to:
• predict the direction of the magnetic force between two parallel, current-carrying wires
• use algebra to find the force F, current I, or separation distance d between two parallel currents when any two of these quantities are given
• use the appropriate right-hand rule to predict the direction of the magnetic field produced by a solenoid
• use algebra to find the magnetic field B, current I, or turns per unit length n when any two of these quantities are given



• Practice:
  Try these additional examples
Example #3

Example #4



• Prepare:
  Read textbook sections 23-1, 23-2 and 23-5 before the next lecture

gc6 20.30
Determine the magnitude and direction of the force between two parallel wires 35 m long and 6.0 cm apart, each carrying 25 A in the same direction.
A. 0.0729 N attractive
B. 0.0729 N repulsive
C. 2.92 N attractive
D. 2.92 N repulsive
Answer















gc6 20.49
A 15-cm-long solenoid that is 1.25 cm in diameter is to produce a field of 0.150 T at its center. How much current should the solenoid carry if it has 575 turns of wire?
A. 94.3 A
B. 31.1 A
C. 12.9 A
D. 9.43 A
Answer















Walker5e 22.64
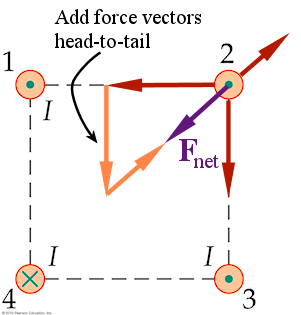
Four wires each carry current I in the directions shown. What is the direction of the magnetic force experienced by wire 2?

(Select the direction indicated by the letters)


Answer















Walker5e 22.53
The number of turns in a solenoid is doubled, and at the same time its length is doubled, while the current remains the same. The strength of the magnetic field within the solenoid will ______.
A. increase
B. decrease
C. stay the same
D. We need to know the current.
Answer























 



A. 0.0729 N attractive





















 



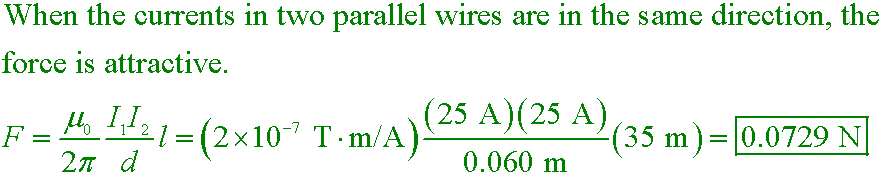
B. 31.1 A





















 



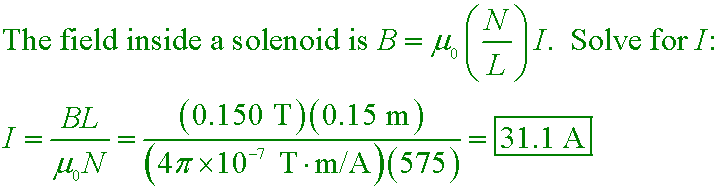
Direction f
Wire 2 will be attracted by wires 1 and 3 but repelled by wire 4. The repulsive force from wire 4 will be smaller than the other two forces because wire 4 is farther away. Adding the vectors head-to-tail reveals a net force toward wire 4, or in the direction indicated by "f".





















 


C. stay the same
Because the number of loops N and the length L each double, the number of loops per unit length n will stay the same and so will the strength of the magnetic field B = μ₀nI.