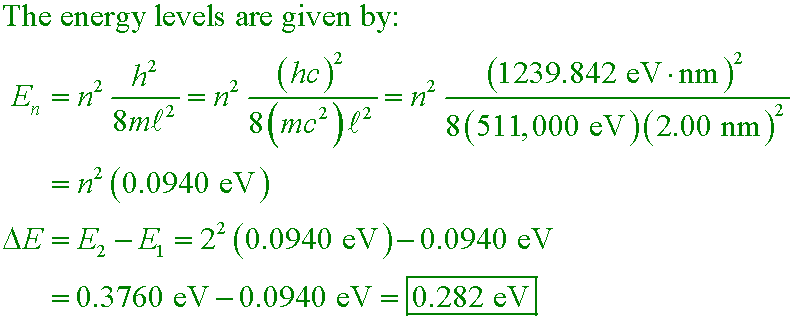Summary

• properties of the wave function
• Schrödinger equation
• Expectation values

• x, p, and E are operators
• Example problem 6.10 continued




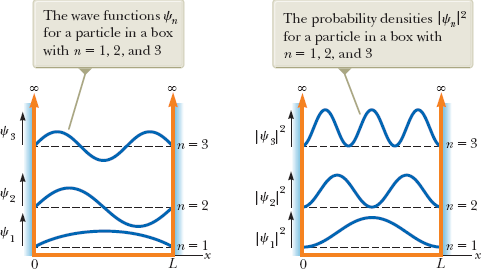
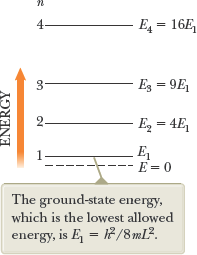
• The particle in a box, part 2
• simple applet
• elaborate applet

• allowed wavelengths
• allowed energies
• Example #6
• Example problem 6.13

Thornton5e 6.10b
A wave function Ψ is A(e^ix + e^−ix) in the region −π < x <π and zero elsewhere. Find the probability of the particle being between x = 0 and x = π/8
A. answer A
B. answer B
C. answer C
D. answer D
Answer

















Thornton5e 6.10c
A wave function Ψ is A(e^ix + e^−ix) in the region −π < x <π and zero elsewhere. Find the probability of the particle being between x = 0 and x = π/4
A. answer A
B. answer B
C. answer C
D. answer D
Answer

















Thornton5e 6.10d
A wave function Ψ is A(e^ix + e^−ix) in the region −π < x <π and zero elsewhere. Calculate the expectation value ⟨x⟩
A. answer A
B. answer B
C. answer C
D. answer D
Answer

















Thornton5e 6.10e
A wave function Ψ is A(e^ix + e^−ix) in the region −π < x <π and zero elsewhere. Calculate the expectation value ⟨x²⟩
A. answer A
B. answer B
C. answer C
D. answer D
Answer

















Thornton5e 6.10f
A wave function Ψ is A(e^ix + e^−ix) in the region −π < x <π and zero elsewhere. Calculate the uncertainty in the particle's position.
A. answer A
B. answer B
C. answer C
D. answer D
Answer

















PSE10 40.07 mod
An electron is contained in a one-dimensional box of length 2.00 nm. How much energy is required to boost it from the n = 1 energy level to the n = 2 level?
A. 0.0940 eV
B. 0.282 eV
C. 0.376 eV
D. 0.564 eV
Answer

















Thornton5e 6.13
Find the average value of psi squared for n = 1, 5, 10, 100, compare with classical
A. answer A
B. answer B
C. answer C
D. answer D
Answer

















PSE10 40.21 (similar to Thornton Example 6.14)
An electron having total energy E = 4.50 eV approaches a rectangular energy barrier with U = 5.00 eV and L = 0.950 nm as shown in the figure. Calculate the probability of tunneling, which is the transmission coefficient.
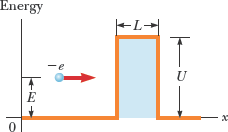A. 5.00×10⁻⁶
B. 3.62×10⁻⁴
C. 1.48×10⁻³
D. 0.0688
Answer

























 



B. Answer B










 



B. Answer B










 



B. Answer B










 



B. Answer B










 



B. Answer B










 



B. 0.282 eV










 



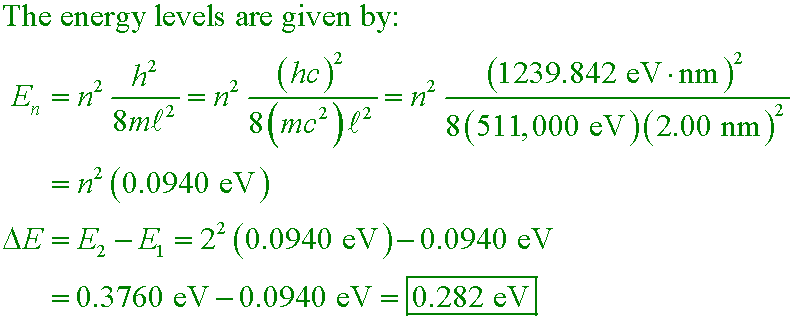
B. Answer B
























 



C. 1.48×10⁻³