Summary

• properties of the wave function
• particle-in-a-box, part 1
• Schrödinger equation

• Review (after spring break, exam 2)
• Foundations of quantum mechanics
• The time-dependent Schrödinger equation T.D.S.E. (Eq. 6.6)
• Ψ(x,t) = Ae^{i(kx − ωt)} is a solution (Problem 6.03)
• Example 6.3 p.209
• Derive the time-independent Schrödinger equation T.I.S.E. (Eq. 6.5)
• Example 6.5 p.211



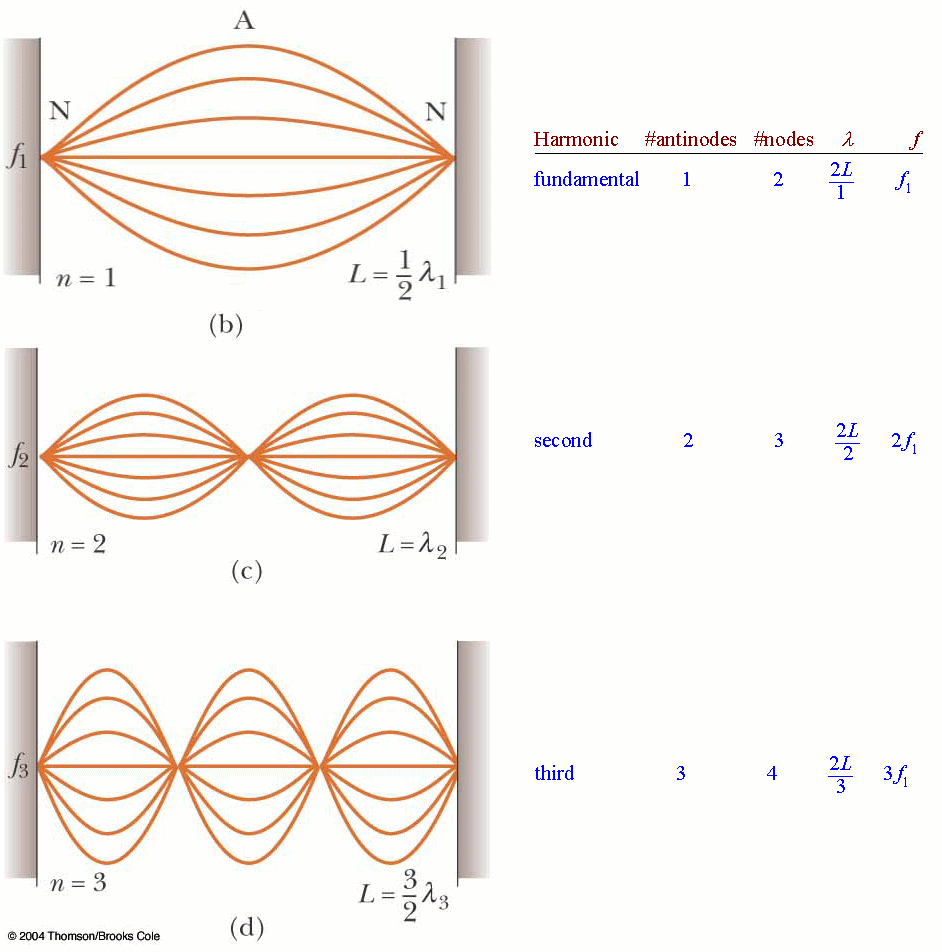
• Standing waves
• Formation by reflection applet
  another animation
• Time-dependent waves add to become a stationary state
• Particle in a box applet (infinite well, mouse=set eigenstate)




• Ray/wave optics analogy to classical/quantum mechanics (pp.212-213)
• Expectation values
• Example problem 6.10a

Thornton5e Example 6.3
Determine whether Ψ(x,t) = Asin(kx − ωt) is a solution to the TDSE.
A. Yes, only if ω = k
B. Yes, always
C. No, never
D. No, unless ω = k
Answer

















Thornton5e Example 6.5
When separating variables, the time-dependent portion equals B·f(t), where B is
A. −13.6 eV
B. ℏω
C. 1/f(t)
D. kx−ωt
Answer

















Thornton5e 6.10a
A wave function Ψ is A(e^ix + e^−ix) in the region −π < x <π and zero elsewhere. Normalize the wave function.
A. A = what
B. A = what
C. A = what
D. A = what
Answer

























 



C. No, never
























 



B. ℏω

























 



A. A = what