Thornton5e 4.04
Thomson worked out many of the calculations for multiple scattering. If the average scattering angle is 1° for alpha-particle scattering, what would be the probability that the alpha particle could scatter by as much as 80° because of multiple scattering? The probability of large-angle scattering is exp[−(θ/θavg)2]
A. 1.56×10−4
B. 1.80×10−35
C. 2.72×10−80
D. 3.28×10−2780
Answer
Thornton5e 4.05b
Calculate the impact parameter for scattering a 7.7-MeV α particle from gold at an angle of 90°
A. 1.69 pm
B. 228 fm
C. 14.8 fm
D. 6.98 fm
Answer
kw5
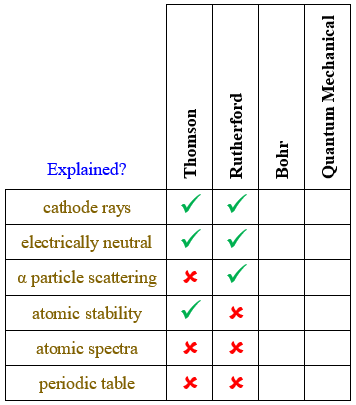
Which of the following is NOT a feature of the Bohr model of the atom?
A. Electrons in planetary-like orbits.
B. Positively charged material surrounding the electrons.
C. Quantized energy levels.
D. Accelerating electrons that do not radiate.
Answer
kw5
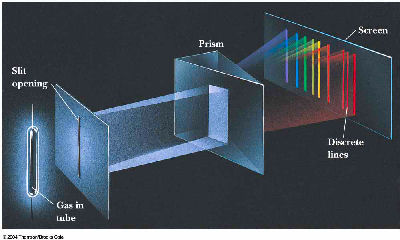
If the electrons in hydrogen atoms are excited to the fourth Bohr orbit, how many different frequencies of light may be emitted?
A. 1
B. 3
C. 4
D. 6
Answer
Walker5 31.29a
Calculate the time required for an electron in the n = 2 state of hydrogen to complete one orbit about the nucleus.
A. 1.21×10−15 s
B. 5.29×10−11 s
C. 9.11×10−9 s
D. 6.63×10−7 s
Answer
Walker5e EYU 31.4
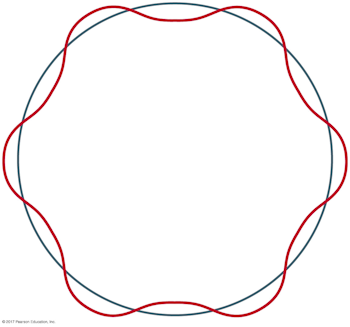
What is the principal quantum number n for the Bohr orbit depicted below?
 A. 1
A. 1
B. 5
C. 6
D. 10
E. 12
Answer
Walker5e 31.03
In the Thomson model of the atom, the mass of an atom is distributed uniformly throughout its volume in a material analogous to pudding. Calculate the density of the "pudding" of a gold atom that has a mass of 3.27×10−25 kg, modeling it as a sphere of radius 0.144 nm.
A. 2.61×104 kg/m³
B. 1.10×105 kg/m³
C. 9.76×108 kg/m³
D. 3.34×1017 kg/m³
Answer
Walker5e EYU 31.3a
If the principal quantum number n is doubled in the Bohr model, the speed of an electron in an orbit _____.
A. is cut to a fourth
B. is cut in half
C. stays the same
D. doubles as well
E. is quadrupled
Answer
D. 3.28×10−2780
Most calculators choke on exp[−6400], and just display zero, but Wolfram Calculator spits out this number.
Geiger and Marsden found that about 1 in 8000 alpha particles were deflected past 90°. The Thomson model, even with multiple scattering, cannot explain the experimental results of Geiger and Marsden!
C. 14.8 fm
Use equation 4.6 p.136 to calculate the impact parameter, with Z1 = 2 and Z2 = 79. Equation 12.2 p.439 predicts the radius of the gold-179 nucleus to be about 6.98 fm, so the alpha particles don't actually touch the nucleus due to the very strong Coulomb repulsion. However, from a quantum-mechanical perspective the outer regions of the wave functions of the alpha particle and the gold nucleus do overlap a tiny bit during the collision. Neither particle can be considered a hard sphere with a definite radius.
B. Positively charged material surrounding the electrons.
The Bohr model retains Rutherford's compact nucleus as the location of all the positive charge in an atom. The Thomson "plum pudding" model is the one that has a positively charged "pudding" surrounding the negatively charged electrons.
D. 6
If the electron jumps from the n = 4 to the n = 3 level, it can then also jump from
3 → 2, 3 → 1, or
2 → 1. Each of those four transitions would release a photon of a unique
energy or color. Two other unique colors would result from 4 → 2 and
4 → 1 jumps, for a total of 6 unique colors.
A. 1.21×10−15 s

Second part of the question:
(b) The typical "lifetime" of an electron in the n = 2 state is roughly
10−8 s; after this time the electron is likely to have dropped back to the
n = 1 state. Estimate the number of orbits an electron completes
in the n = 2 state before dropping to the ground state.


C. 6
A careful accounting of the complete wavelengths that span the circumference of the orbit reveals there are six, which corresponds to the value of the principal quantum number.
A. 2.61×104 kg/m³

This "pudding" is 13 trillion times less dense than an alpha particle, which has a density of approximately 3.3×1017 kg/m³. That is why the scattering of alpha particles from gold foil proved the atoms must have a small, dense nucleus. Thomson's "pudding" would never stop an alpha particle, let alone scatter it backward!
B. is cut in half
As seen in Equation 31-6, the speed of an electron in a Bohr orbit is inversely proportional to the principal quantum number n.






 A. 1
A. 1



