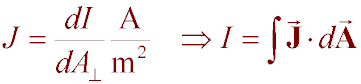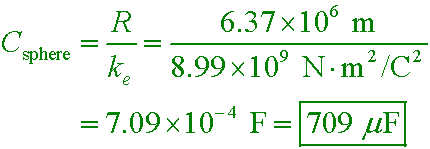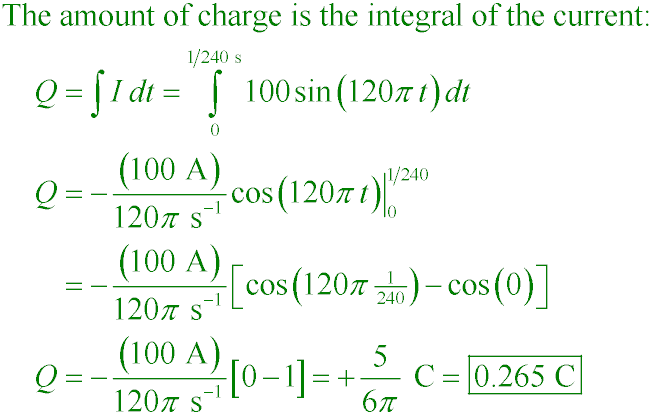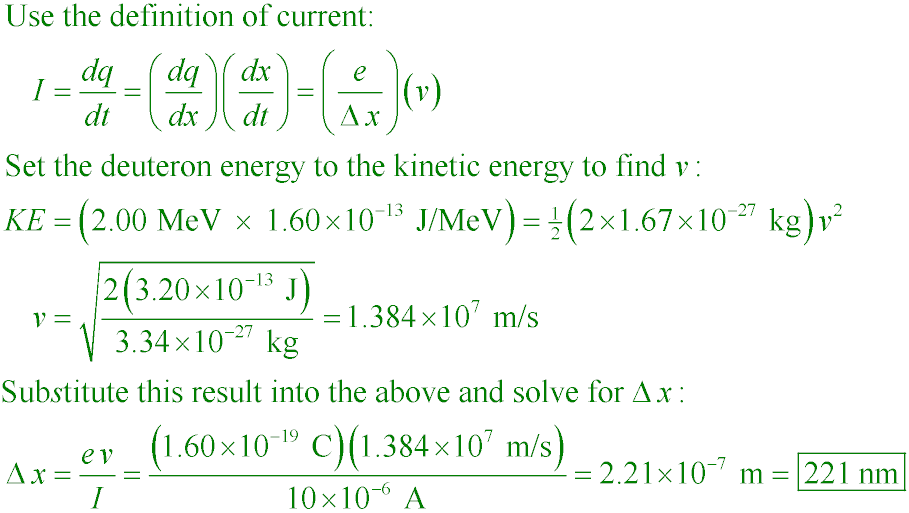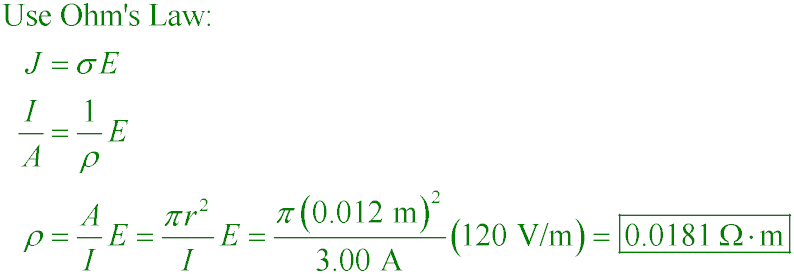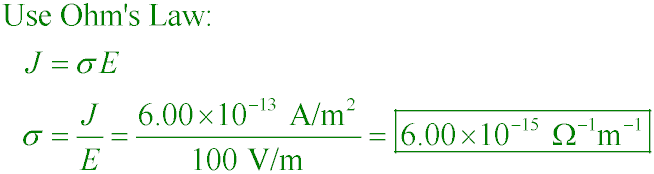klm
If you model the Earth as a spherical conductor of radius RE = 6370 km, what is its capacitance?
A. 225 pF
B. 188 nF
C. 709 µF
D. 822 mF
Answer
PSE10 QQ 26.1
Rank the magnitudes of the currents in the four regions, from lowest to highest.
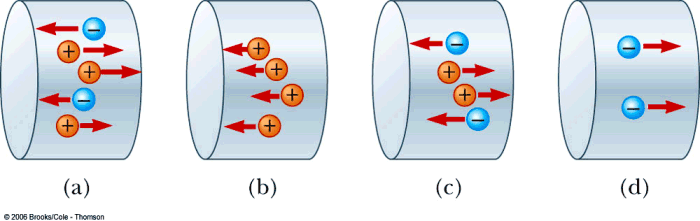
A. c < a < d < b
B. d < c < b < a
C. a = c = d < b
D. d < b = c < a
Answer
PSE10 26.09
What total charge is carried by current
I(t) = (100 A) sin (120πt)
in the time from t = 0 to t = 1/240 s?
A. 67.7 µC
B. 13.5 mC
C. 0.265 C
D. 1.85 C
Answer
PSE10 26.08
A beam of 2.00 MeV deuterons (charge +1e) has a current of 10 µA. How far apart
are the deuterons?
A. 221 nm
B. 17.8 µm
C. 0.765 mm
D. 1.18 cm
Answer
PSE6 27.16
A 1.20-cm radius conductor carries 3.00 A of current that is driven by E = 120 V/m. What is the
resistivity of the conductor?
A. 0.772 Ω·m
B. 0.373 Ω·m
C. 0.112 Ω·m
D. 0.0181 Ω·m
Answer
PSE10 26.15
An atmospheric current density of 6.00×10−13 A/m2 exits at a location
where E = 100 V/m. What is the atmospheric conductivity in this region?
A. 6.00×10−15 (Ω·m)−1
B. 7.50×10−14 (Ω·m)−1
C. 1.20×10−12 (Ω·m)−1
D. 5.85×10−10 (Ω·m)−1
Answer
Walker5e 21.21

A potential difference V is applied to a conducting block of height A, width B,
and length C as shown above. Current IAB flows when V
is applied to the faces AB. What is the current when V is applied to the faces BC?
A. (AB/BC)IAB
B. (A²B²C²)IAB
C. (C²/A²)IAB
D. IAB
Answer
Walker5e EYU 21.2
If the voltage and resistance are each doubled in a simple battery-resistor circuit, the current will _____.
A. double
B. stay the same
C. be cut in half
D. be cut to a fourth
Answer
C. 709 µF
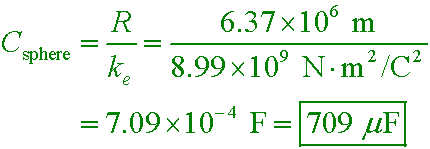

D. d < b = c < a
A positive charge moving to the right contributes the same current
as a negative charge moving to the left. Therefore, we see that (a) represents 5 units of current to
the right, (b) is four units of current to the left, (c) is four units of current to the right, and
(d) is two units of current to the left. Ignoring the direction and ranking only the
magnitude of the current, we arrive at ranking D.
C. 0.265 C
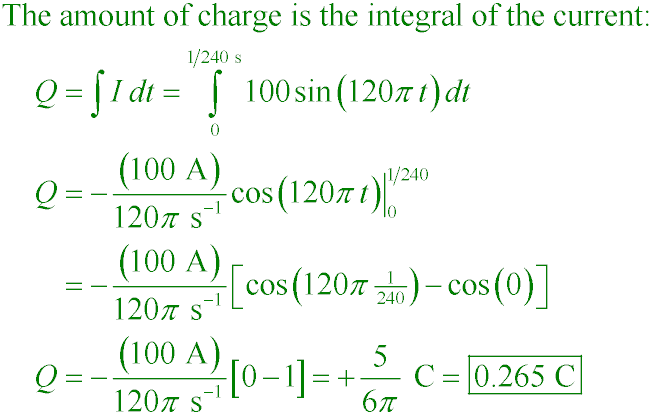
A. 221 nm
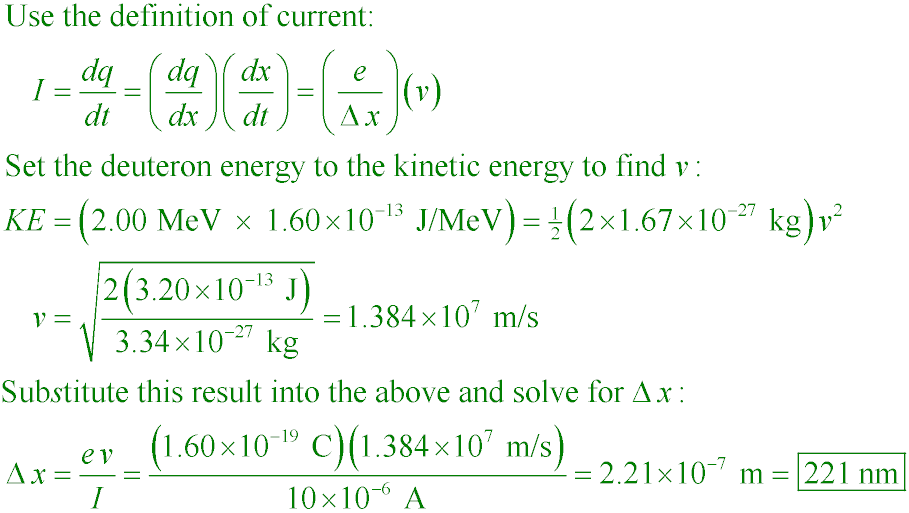
D. 0.0181 Ω·m
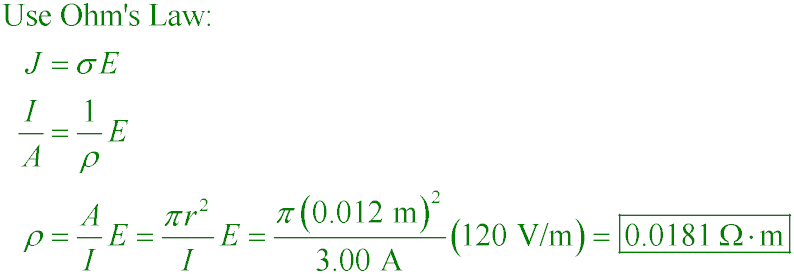
A. 6.00×10−15 (Ω·m)−1
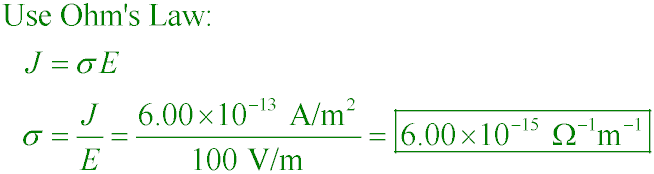
C. (C²/A²)IAB
B. stay the same
You can support this answer algebraically with I = ΔV/R, or by remembering the potential difference drives the current and the resistance impedes the current. If both the driving force and impedance increase by the same amount, there will be no change in the current.