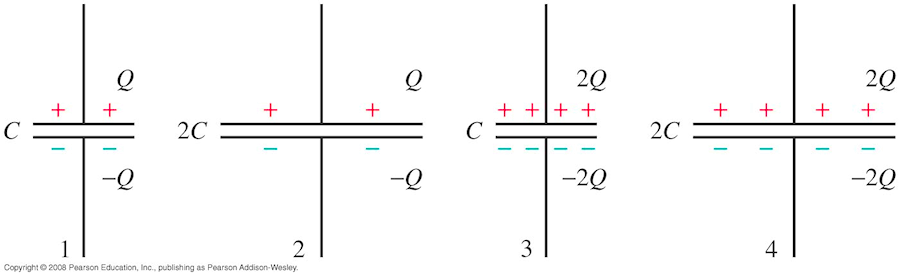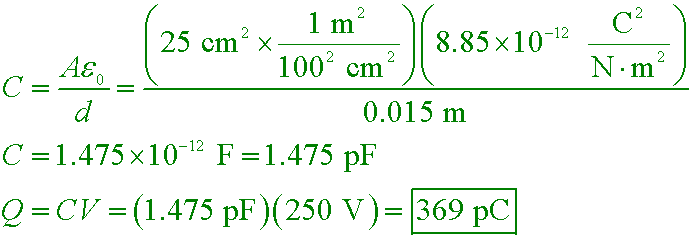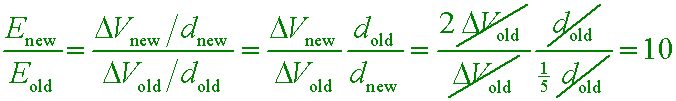Summary

• Potential due to distributed charges
• Potential and conductors
• Concentric shells example

---

Chapter 25

---



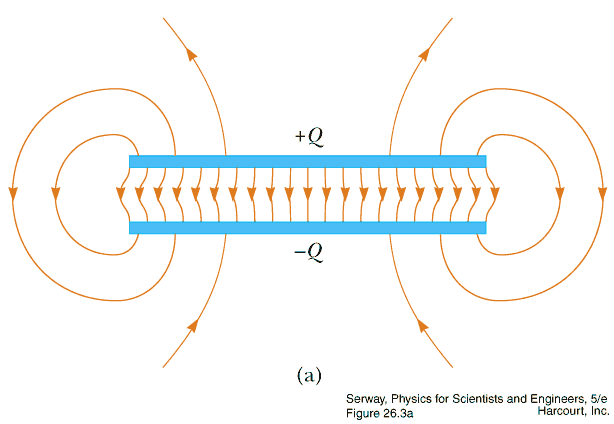
• Capacitance
  • definition
  • calculating
  
  Example #1
  



• Practice:
  Try these additional examples

Example #2

Example #3



• Prepare:
  Read textbook sections 25-3 before the next lecture

Knight2 30.Q.12
Rank in order, from largest to smallest, the potential differences across these capacitors.

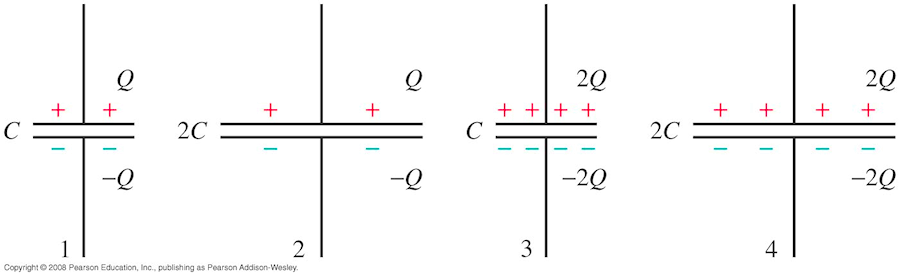
A. ΔV₄ > ΔV₃ > ΔV₂ > ΔV₁
B. ΔV₁ = ΔV₄ > ΔV₃ > ΔV₂
C. ΔV₂ > ΔV₁ = ΔV₄ > ΔV₃
D. ΔV₃ > ΔV₁ = ΔV₄ > ΔV₂
Answer















sb5 26.47
A capacitor with A = 25 cm² and d = 1.5 cm is charged to 250 V. What is the charge on its plates?
A. 151 nC
B. 369 pC
C. 519 µC
D. 17.1 mC
Answer















APB 1998.14
Two parallel conducting plates are connected to a constant voltage source. The magnitude of the electric field between the plates is 2,000 N/C. If the voltage is doubled and the distance between the plates is reduced to 1/5 the original distance, the magnitude of the new electric field is
A. 800 N/C
B. 1,600 N/C
C. 2,400 N/C
D. 5,000 N/C
E. 20,000 N/C
Answer





































 



D. ΔV₃ > ΔV₁ = ΔV₄ > ΔV₂

Apply the expression ΔV = Q/C to find the potential difference across each capacitor and then compare the results.




















 



B. 369 pC





















 



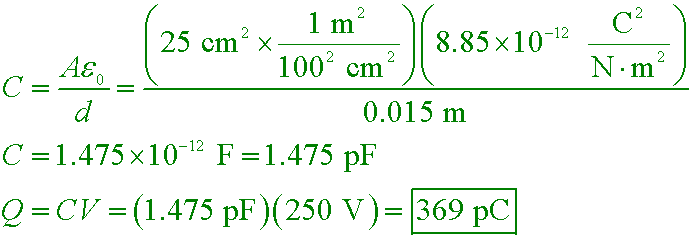
E. 20,000 N/C

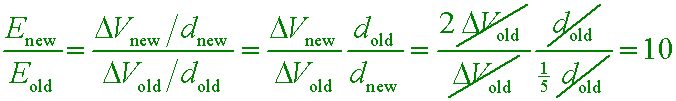
The electric field is uniform and constant between the plates and equals ΔV/d (Eq. 20-4, see also Eq. 20-11). Doubling ΔV will double E, and decreasing d by a factor of 5 will increase E by a factor of 5. The two changes together will increase E by a factor of 10.