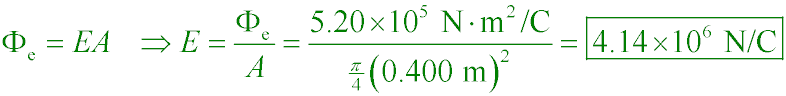Summary
- Continuous charge distributions
- Ring of charge
- Charged particle motion
Knight2 27.cq.02
In which location(s) in this figure might the electric field E be zero?

1. A, B, or C
2. A or B
3. B or C
4. B only
5. C only
Answer
POP4 19.31
The maximum flux through a 40.0-cm-diameter loop that is rotated in a uniform field is
ΦE = 5.20×105 N·m2/C.
What is E?
A. 65.3 kN/C
B. 4.14 MN/C
C. 1.03 MN/C
D. 8.28 GN/C
Answer
PSE6 24.13
Calculate the electric flux that leaves the closed paraboloidal surface shown in the figure.
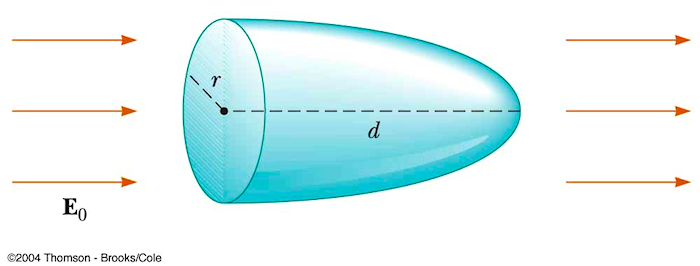
A. E0π(d 2 + r 2)
B. E0πr 2/d 2
C. E0πr 2d 2
D. E0πr 2
Answer
5. C only
The larger magnitude of the positive charge will result in a nonzero
field everywhere to its left because the negative charge will be too small and too far away. That rules
out location A. In between the two charges the fields add, not subtract, so that rules out B. The only
possibility is location C, where the nearby negative charge's field can cancel out the field from the
more distant positive charge.
B. 4.14 MN/C
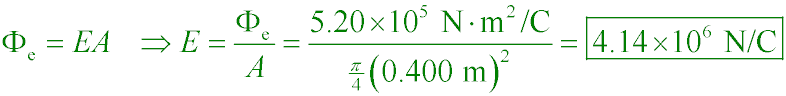
D. E0πr 2
There is no charge inside the surface (it is empty... plus, if
there were charge inside the electric field could not be uniform) so whatever flux enters the
surface must also leave the surface. It is easiest to calculate the flux entering the lefthand, circular
side of the surface, the area of which is πr2.