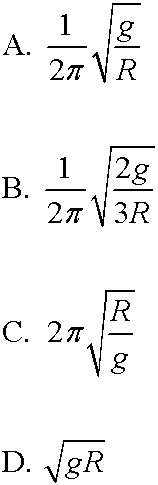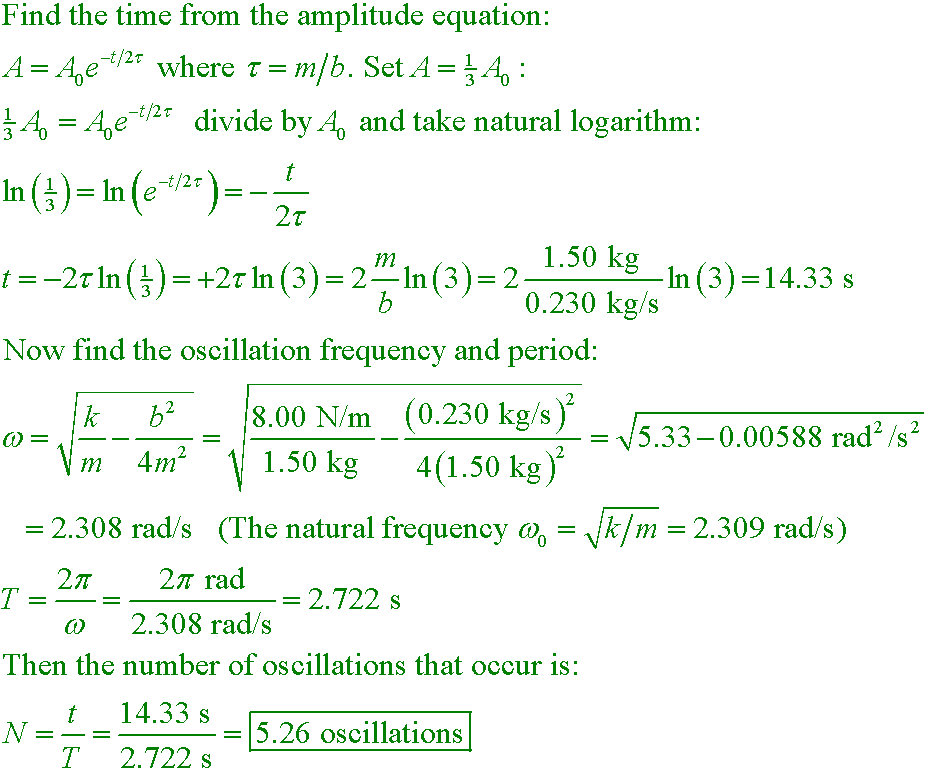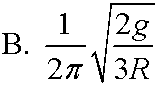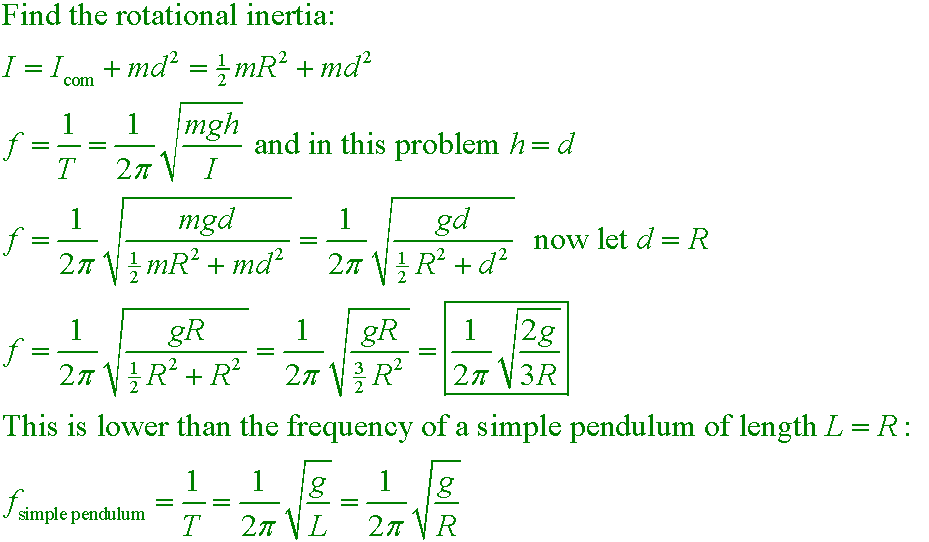Summary
- Oscillatory motion
- Mass on spring
- Energy and oscillations
Bonus question Ch.14
- Written Quiz Ch.14
- The physical pendulum
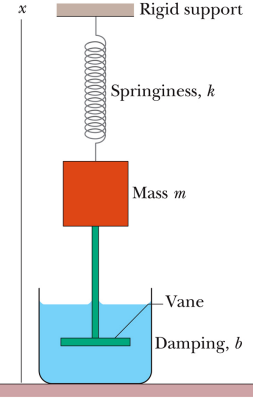
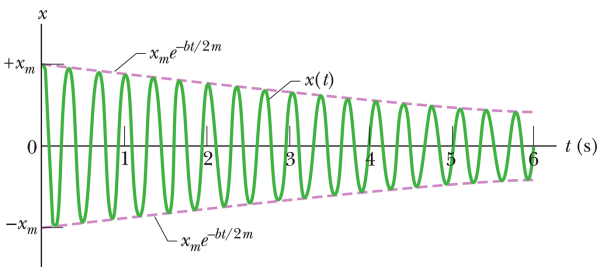
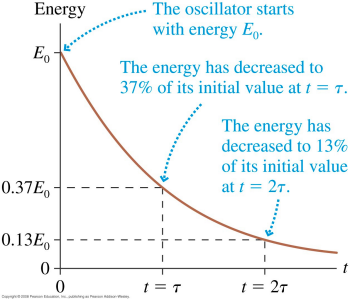
- Damped oscillations
- differential equations
- damping constant b
- reduced frequency, lengthened period
- exponential decay of energy
Example #1
Example #2
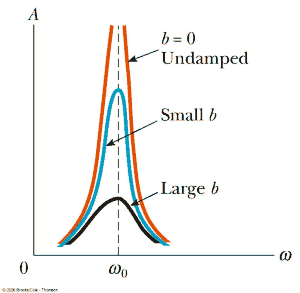
- Resonance

pse6 14.34
A frog in a 6.00-cm radius hemispherical pod barely floats in a pool of ρ = 1350 kg/m3
blue-green ooze. If the pod has negligible mass, what is the mass of the frog?

A. 611 g
B. 323 g
C. 898 g
D. 1.12 kg
Answer
klm
Which of the following displacement functions x(t) would best correspond to a damped oscillator with a damping constant of b = 0?
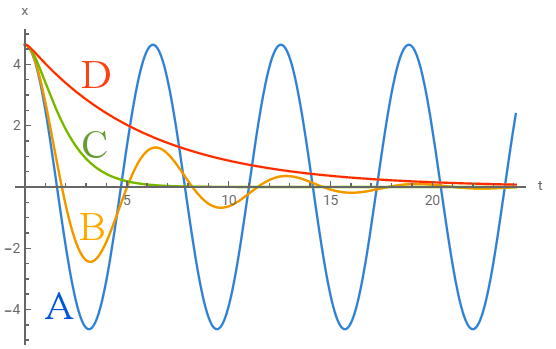 A. function A
A. function A
B. function B
C. function C
D. function D
Answer
HRW10e 15.59
For the damped oscillator shown, m = 1.50 kg, k = 8.00 N/m, and b = 0.230 kg/s. The block is pulled down 12.0 cm and released. How many oscillations does the block make before its amplitude falls to one-third its initial value?
 A. 0.785 oscillations
A. 0.785 oscillations
B. 1.05 oscillations
C. 5.26 oscillations
D. 14.3 oscillations
Answer
HRW10e 15.47mod
At what frequency f should a uniform solid disk of radius R, pivoting about an axis a distance d = R from its center (at the disk's edge), be driven to maximize the amplitude of its oscillation?
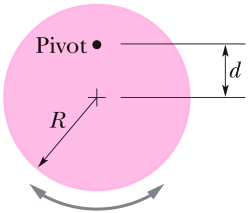
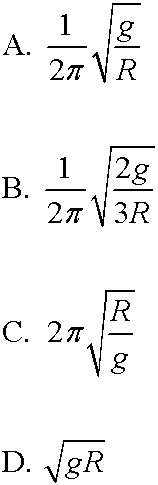
Answer
answer
A. 611 g

answer

A. function A
If b = 0 then no damping occurs, and the oscillator amplitude and energy remain constant.
answer
C. 5.26 oscillations
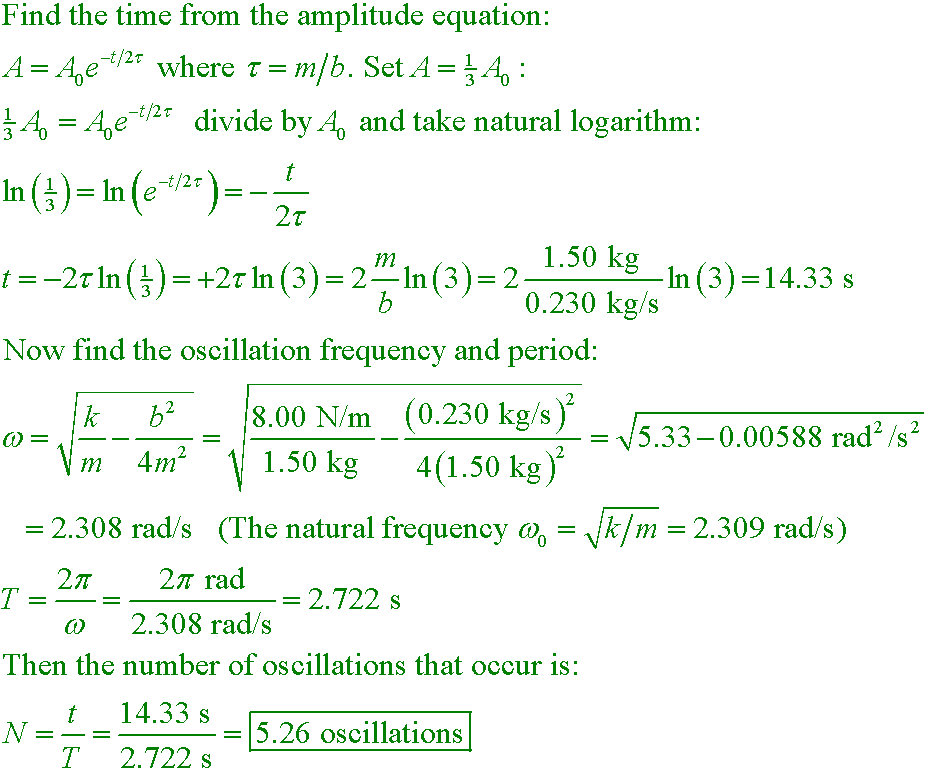
answer
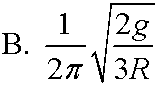
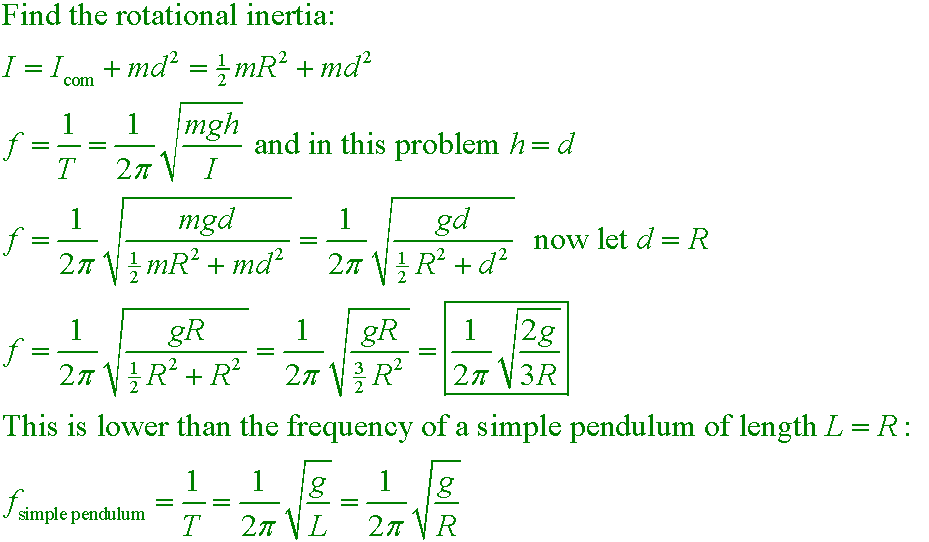











 A. function A
A. function A A. 0.785 oscillations
A. 0.785 oscillations