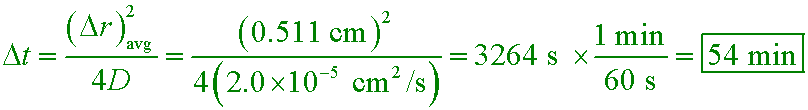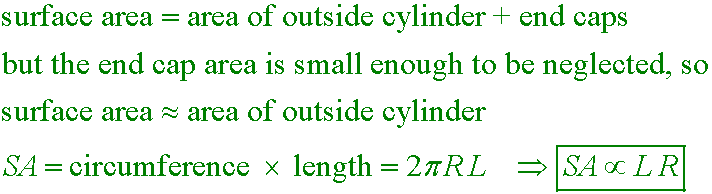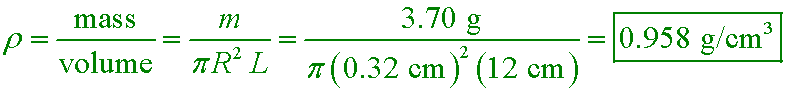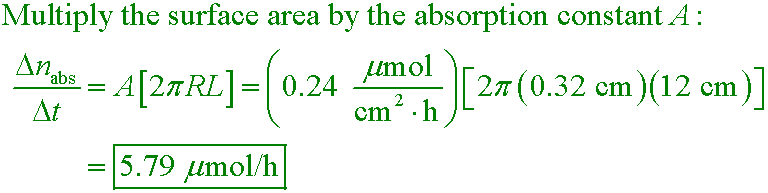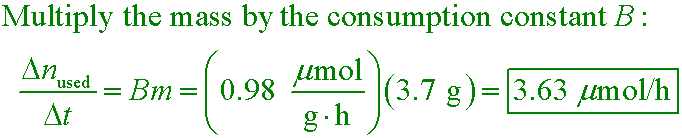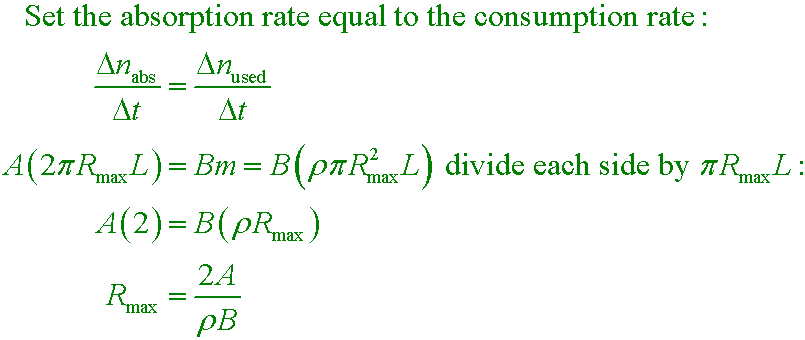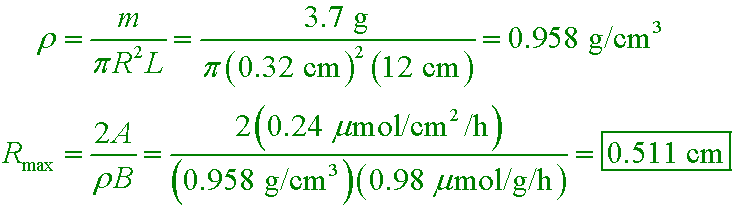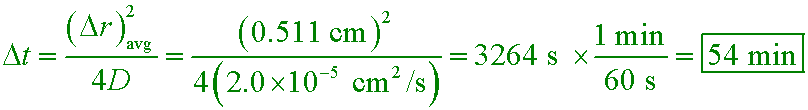Summary

• Holography
• Diffusion
• Fick's first law
• Einstein-Smoluchowski

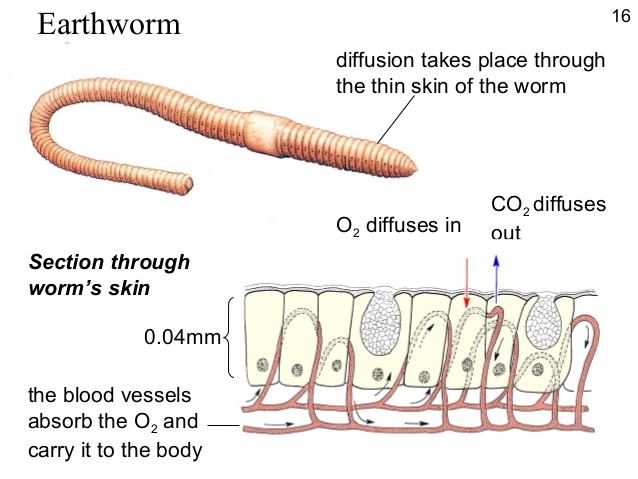
• Oxygen diffusion
• Oxygen diffusion and animals slides
• Maximum size of a worm
Example #1
Example #2
Example #3
Example #4
Example #5
Example #6
Example #7
Example #8



• Lecture learning outcomes
  A student who masters the topics in this lecture will be able to:
• describe how the balance between oxygen supply and oxygen demand, together with the oxygen diffusion rate through tissues, determines the maximum dimensions of an animal that lacks a circulatory system



• Prepare:
  Read the textbook sections 30-1 and 30-2 before the next lecture

oxygen diffusion in B.1
How does the surface area of a worm depend on its length L and radius R?
A. Surface area ∝ LR²
B. Surface area ∝ LR
C. Surface area ∝ 1⁄_LR
D. Surface area ∝ 1⁄_LR²
Answer















oxygen diffusion in B.2
How does the volume of a worm depend on its length L and radius R?
A. Volume ∝ LR²
B. Volume ∝ LR
C. Volume ∝ 1⁄_LR
D. Volume ∝ 1⁄_LR²
Answer















oxygen diffusion A.3
If a worm has the dimensions m = 3.7 g, L = 12 cm, and R = 0.32 cm, what is its density?
A. 138 g/cm³
B. 3.70 g/cm³
C. 1.04 g/cm³
D. 0.958 g/cm³
Answer















oxygen diffusion in C.1
If a worm has the dimensions m = 3.7 g, L = 12 cm, and R = 0.32 cm, at what rate can it absorb oxygen if A = 0.24 µmol/cm²/h? Ignore the contribution from its "end caps."
A. 0.00995 µmol/h
B. 0.154 µmol/h
C. 1.84 µmol/h
D. 5.79 µmol/h
Answer















oxygen diffusion in C.2
If a worm has the dimensions m = 3.7 g, L = 12 cm, and R = 0.32 cm, at what rate does its body use oxygen if B = 0.98 µmol/g/h?
A. 0.265 µmol/h
B. 0.626 µmol/h
C. 3.63 µmol/h
D. 13.4 µmol/h
Answer















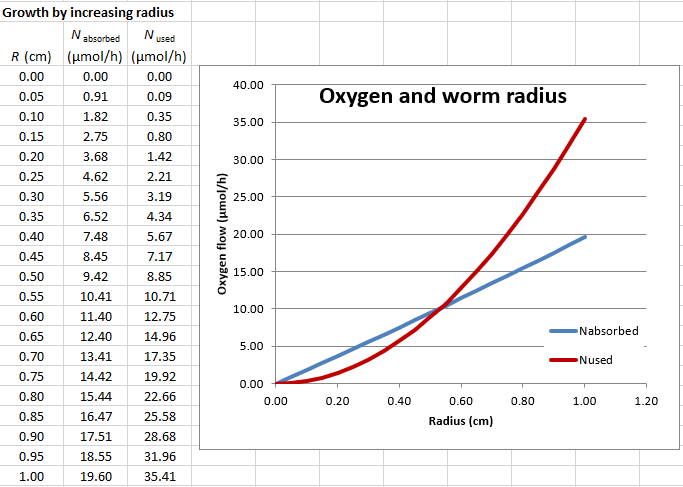
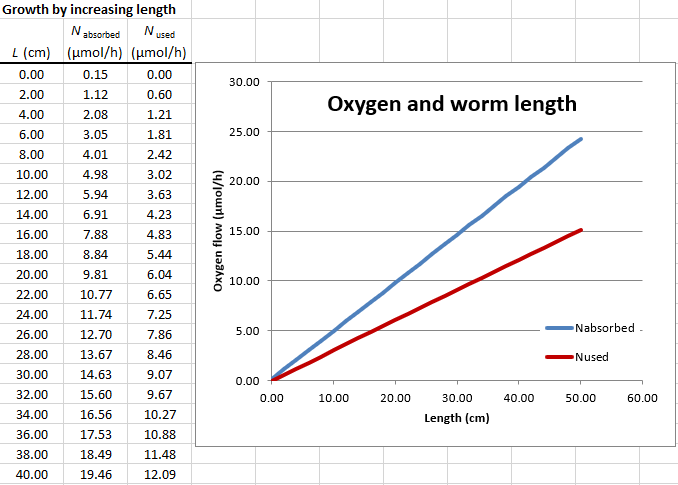
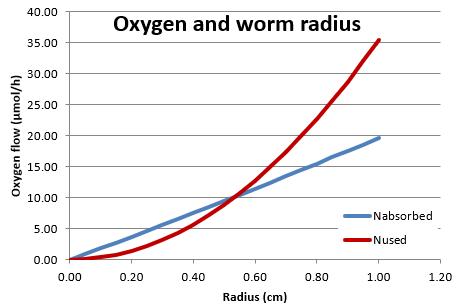
oxygen diffusion in D.1 and D.2
Use Excel to construct graphs of oxygen absorbed and oxygen consumed as functions of worm radius and length. Do the curves cross?
Answer















oxygen diffusion in D.3
Let the rate of oxygen absorption match the rate of consumption in the worm. We learn that if A were larger then R_max is _____, and if B were larger then R_max is _____.
A. larger ... larger
B. larger ... smaller
C. smaller ... larger
D. smaller ... smaller
Answer















oxygen diffusion in worms E.2
What is the maximum radius of a worm when modeled in this way?
A. 0.0715 cm
B. 0.163 cm
C. 0.511 cm
D. 1.96 cm
Answer















oxygen diffusion in worms extra insight
If a worm had no circulatory system and must diffuse oxygen all the way from its skin to its center, how much time would it take the average oxygen molecule to diffuse 0.511 cm? Let D = 2.0×10⁻⁵ cm²/s, and model the process as two-dimensional diffusion.
A. 91 s
B. 54 min
C. 9.1 h
D. 1.8 days
Answer























 



B. Surface area ∝ LR
























 



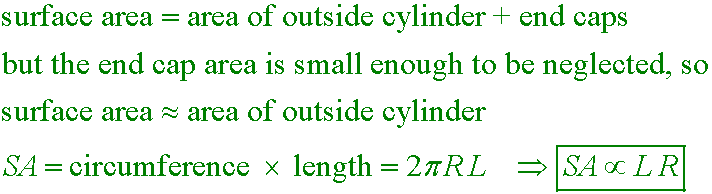
A. Volume ∝ LR²
























 



D. 0.958 g/cm³






















 



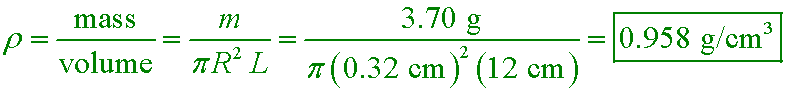
D. 5.79 µmol/h






















 



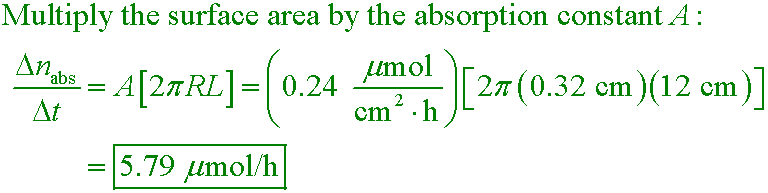
C. 3.63 µmol/h






















 



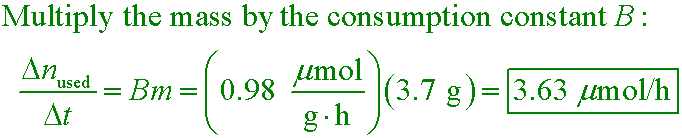
B. larger ... smaller






















 



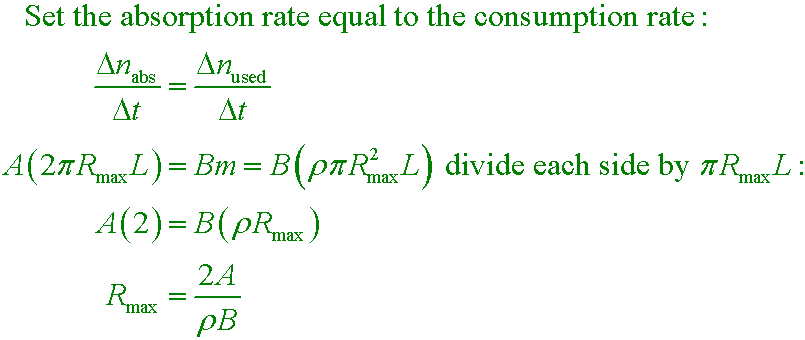
C. 0.511 cm






















 



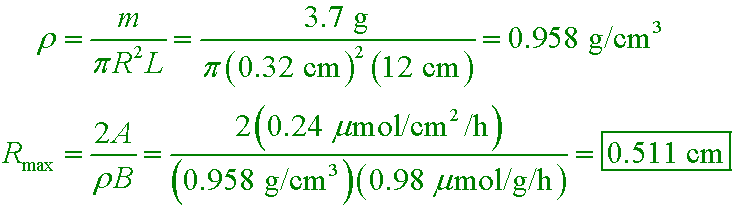
B. 54 min