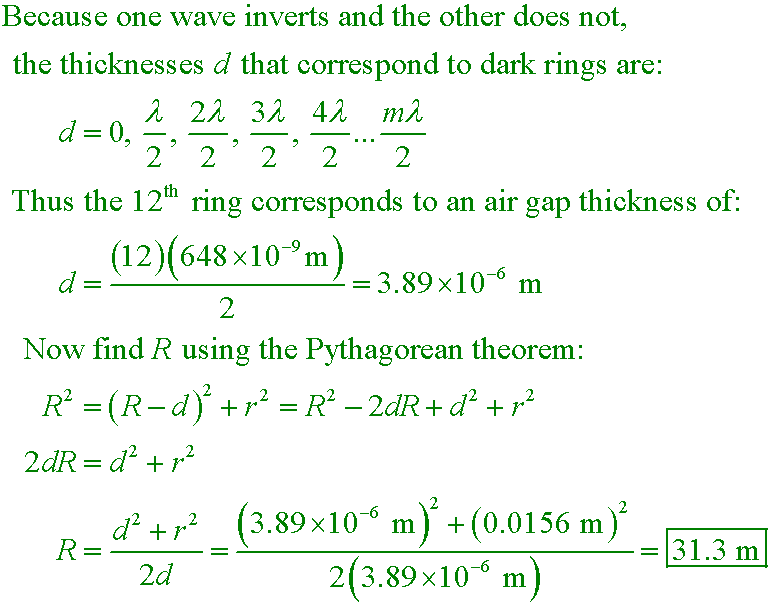Summary

• Human vision correction
• Magnifying glass
• Two-source interference

• Quiz Bonus Chs.26-27


   



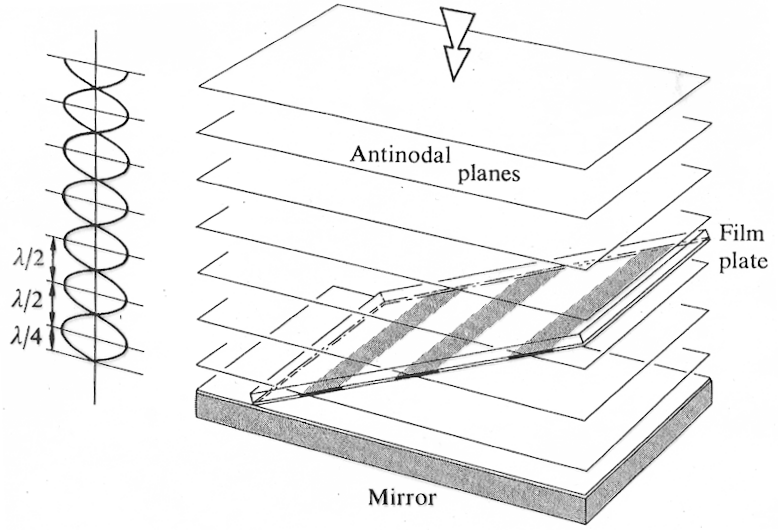
• Thin film interference

• wave inversion applet
• thin film diagram
• soap bubbles

Example #1

Example #2


• microscope slides (wedge fringes)
• Newton's rings

Example #3


  


• Lecture learning outcomes
  A student who masters the topics in this lecture will be able to:
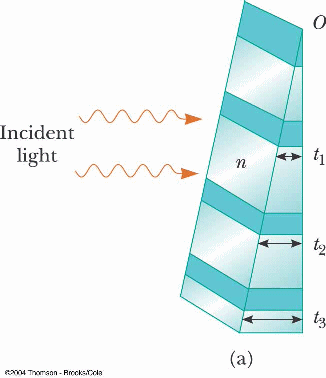
• describe how colors of light reflected by a thin film can be explained in terms of wave interference
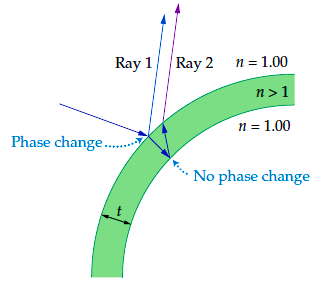
• use given boundary conditions to predict wave inversion or no inversion upon reflection
• distinguish bright reflection (constructive interference) from anti-reflection (destructive interference) when solving for wavelength or film thickness in a thin film interference problem
• use algebra to find the film thickness t, order number m, or wavelength in the film λ_n for thin film interference when any two of these quantities are given



• Practice:
  Try these additional examples
Example #4

Example #5



• Prepare:
  Read textbook section 28-4 before the next lecture

POP5 26.qq.6
A converging lens forms a sharp image of a candle. If you cover the top half of the lens with a piece of paper, what happens to the appearance of the image?
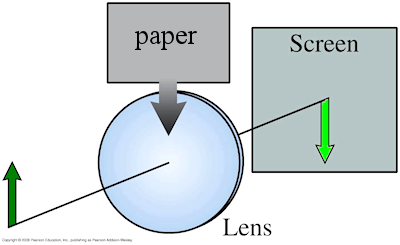
A. The bottom half disappears.
B. The top half disappears.
C. The entire image is visible but dimmer.
D. The entire image inverts upside-down.
Answer















kw4
Why don't we notice interference patterns when we turn on two lights in a room?
A. The lights aren't in phase.
B. The lights are too bright.
C. The lights are too dim.
D. The air molecules disturb the interference pattern.
Answer















gc6 24.76
How thick should an antireflection coating (n = 1.38) on glass (n = 1.52) be in order to suppress reflection of λ = 515 nm light?
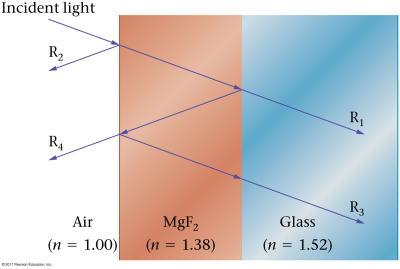A. 93.3 nm
B. 129 nm
C. 187 nm
D. 258 nm
Answer















Walker5e 28.36
Monochromatic light with λ = 648 nm shines down on a plano-convex lens lying on a piece of plate glass, as shown below. When viewing from above, one sees a set of concentric dark and bright fringes, referred to as Newton's rings. If the radius of the twelfth dark ring from the center is measured to be 1.56 cm, what is the radius of curvature, R, of the lens?

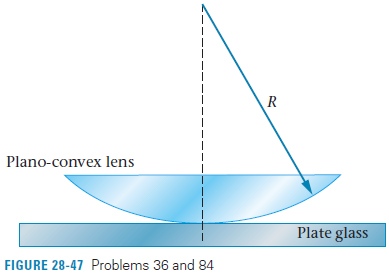
A. 1.28 m
B. 31.3 m
C. 74.4 mm
D. 3.89 µm
Answer















Walker5e CnEx 28-5
Interference fringes are formed when light shines on an air wedge. Is the point where the glass plates touch a dark fringe or a bright fringe?

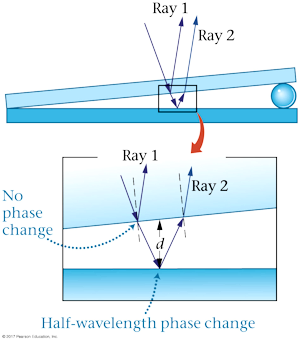
A. dark fringe
B. bright fringe
C. It depends on the index of refraction of the glass.
Answer


















Walker5e RWP Fig 28-21
What is the minimum height h of a "bump" on a DVD that will produce destructive interference when illuminated by half of the λ = 780 nm laser beam (center figure)?
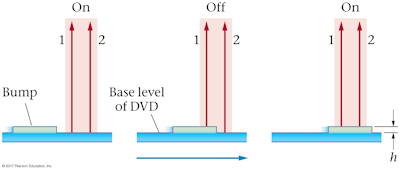
A. 1560 nm
B. 780 nm
C. 390 nm
D. 195 nm
Answer























 



C. The entire image is visible but dimmer.
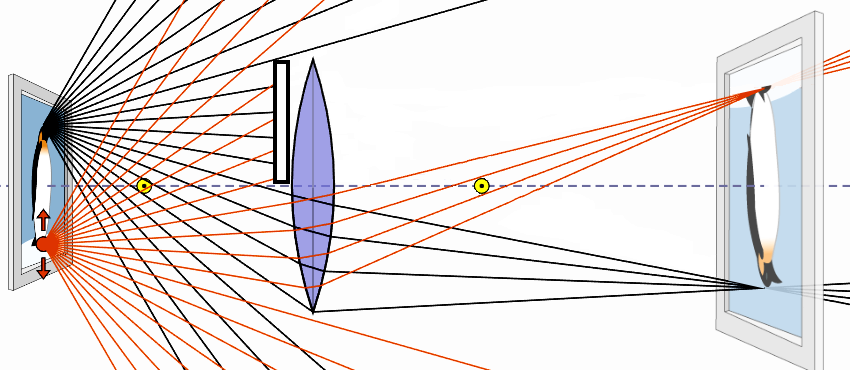
The paper blocks half of the light rays and the image becomes dimmer. However, the other half of the lens still directs rays to every part of the real image of the candle, so the entire image is visible. This is an example of an aperture stop, which limits the total amount of light that passes through a system (like the aperture setting of a camera). A field stop at the film plane (the location of the real image) would indeed block half of the image.

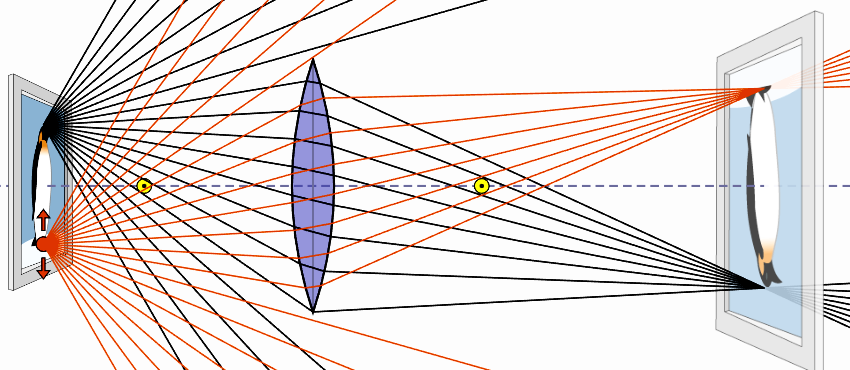
Ray diagram with the lens unblocked:


Ray diagram with the lens half blocked:






















 



A. The lights aren't in phase.
In order to see constructive and destructive interference, there must be a fixed phase relationship between the waves coming from various sources. There is no such relationship for light waves emitted from two different light bulbs. The light bulbs also emit many different wavelengths simultaneously, further complicating efforts to detect wave interference.




















 



A. 93.3 nm

See also Quick Example 28-8 p. 995.




















 



B. 31.3 m



























 



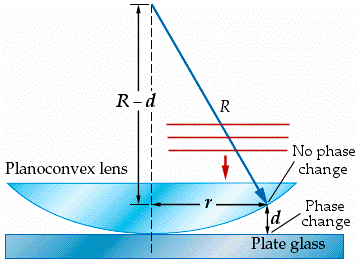
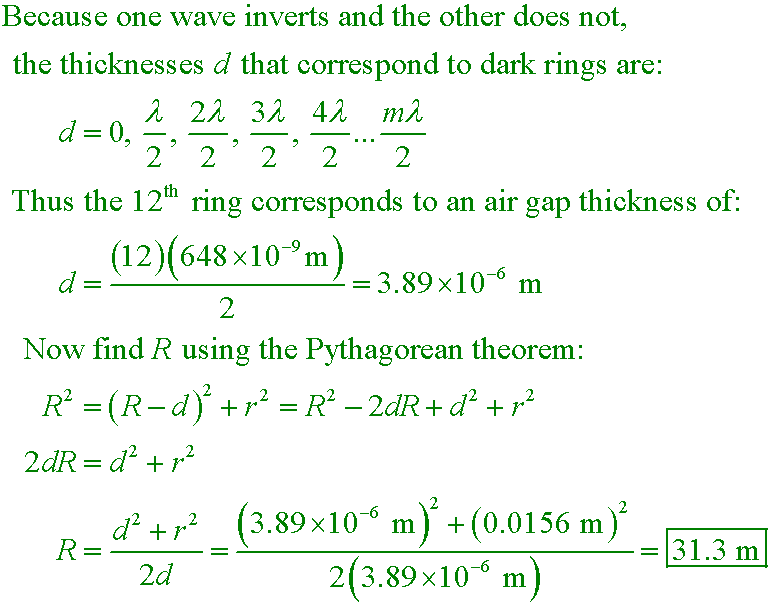
A. dark fringe
Ray 1 undergoes no phase change on reflection, whereas ray 2 experiences a 180° phase change due to reflection. It follows, then, that when the path difference 2d approaches zero at the point where the glass plates touch, rays 1 and 2 will cancel with destructive interference.





















 



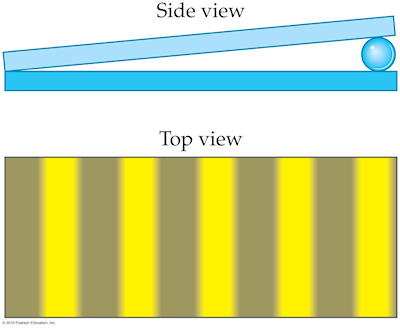
D. 195 nm
A bump of minimum height h = λ/4 will force beam 2 to travel half a wavelength farther than beam 1 in the center figure, producing destructive interference between the reflected waves from each beam. The minimum height is thus (780 nm)/4 = 195 nm.