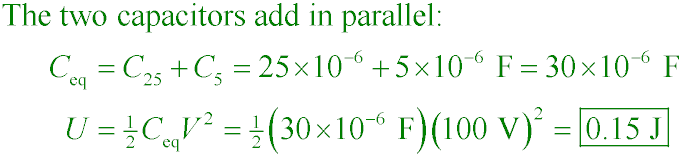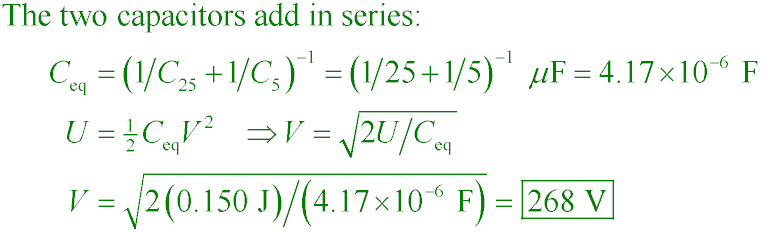Summary

• Ohm's Law
• Electric power
• Kirchhoff's rules

• Written Quiz Ch. 20




---

End of material on Exam I

---



• Circuits with capacitors
• Capacitors in series and in parallel
Example #1
Example #2


• Charging and discharging in RC circuits applet
• An uncharged capacitor is like a wire
• A charged capacitor is like an open circuit


• Circuit Applet for flashlamp circuit (problem 21.80)


• Nerve impulse propagation speed (problem 21.81) Example #3
  Example #4
  Example #5
  
  
  



• Lecture learning outcomes
  A student who masters the topics in this lecture will be able to:
• calculate the equivalent capacitance of capacitors connected in series or connected in parallel
• use characteristics of uncharged and charged capacitors to predict the behavior of simple resistor-capacitor circuits both immediately after a battery is connected and a long time after the battery is connected
• [We will not study the RC time constant or the time-dependent exponential behavior of resistor-capacitor circuits.]



• Practice:
  Try these additional examples
Example #6

Example #7

Example #8



• Prepare:
  Read textbook section 22-1 before the next lecture

POP4 20.49
Two capacitors of 25 µF and 5 µF are connected in parallel with 100 V across each. What is the total energy stored?
A. 150 µJ
B. 0.150 J
C. 150 J
D. 150 kJ
Answer













POP4 20.49
Two capacitors of 25 µF and 5 µF are connected in series. What ΔV is required to store 0.150 J?
A. 22.8 V
B. 100 V
C. 137 V
D. 268 V
Answer













Walker5e 21.81
The speed that nerve impulses travel is given by v = L/RC, where L = 0.0010 m is the length of an axon, R = 2.55×10⁷ Ω is its resistance, and C is its effective "wall capacitance." The presence of a myelin sheath decreases the wall capacitance from 314×10⁻¹² F (314 pF)to only 1.57×10⁻¹² F (1.57 pF). The myelinated axons therefore support a ____ speed of ____.

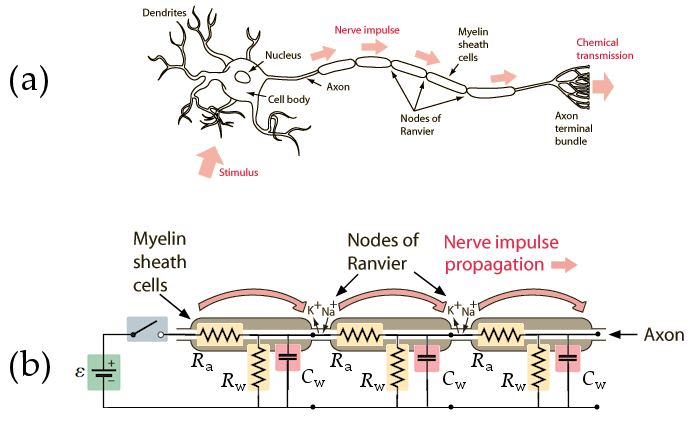
A. higher ... 25.0 m/s
B. higher ... 63.7 m/s
C. lower ... 25.0 m/s
D. lower ... 63.7 m/s
Answer















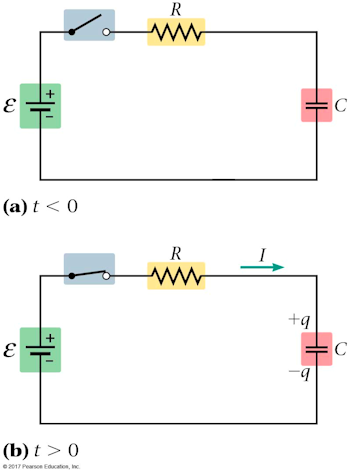
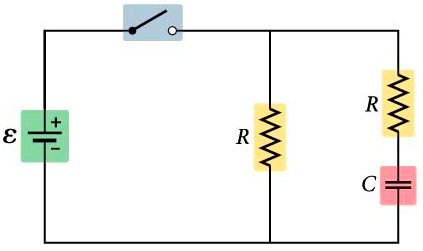
klm Walker5e CnEx 21-19
The switch in the figure below is initially open and the capacitor is uncharged. If ℰ = 6.00 V, R = 10.0 Ω, and C = 72.0 µF, what current flows through the battery immediately after the switch is closed?
circuit simulator

A. 0.432 mA
B. 0.600 A
C. 0.900 A
D. 1.20 A
Answer















klm Walker5e CnEx 21-19
The switch in the figure below is initially open and the capacitor is uncharged. If ℰ = 6.00 V, R = 10.0 Ω, and C = 72.0 µF, what current flows through the battery a long time after the switch is closed?

A. 0.432 mA
B. 0.600 A
C. 0.900 A
D. 1.20 A
Answer















klm Walker5e Ex 21-17
If C = 24.0 µF in the circuit below, what is the equivalent capacitance of the entire circuit?

A. 8.00 µF
B. 16.0 µF
C. 36.0 µF
D. 72.0 µF
Answer















Walker5e 21.61
Two capacitors, C₁ = C and C₂ = 2C, are connected to a battery. Capacitor _____ stores more energy when they are connected to the battery in series and capacitor _____ stores more energy when they are connected in parallel with the battery.
A. C₁ ... C₁
B. C₂ ... C₁
C. C₁ ... C₂
D. C₂ ... C₂
Answer







sj6 28.33
The battery has been connected to the circuit below for a long time. What is the voltage across the capacitor?
A. 2.00 V
B. 4.00 V
C. 6.00 V
D. 8.00 V
Answer























 



B. 0.150 J




















 



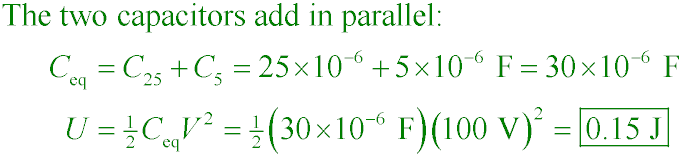
D. 268 V




















 




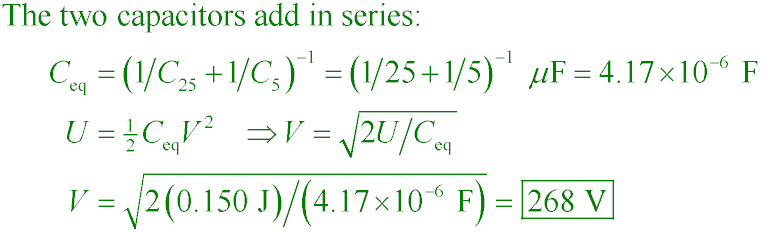
A. higher ... 25.0 m/s




















 



D. 1.20 A

Immediately after the switch is closed the capacitor is uncharged and behaves like a wire. The 6.00-V battery drives 0.600 A of current through each of the 10.0-Ω resistors (or, if you prefer, the two resistors in parallel have an equivalent resistance of 5.00 Ω) resulting in 1.20 A flowing through the battery.



















 



B. 0.600 A

A long time after the switch is closed the capacitor is fully charged and behaves like an open circuit. The 6.00-V battery drives 0.600 A of current through the left-hand 10.0-Ω resistor.


















 



C. 36.0 µF

The two capacitors in series have an equivalent capacitance of ½C, and they are connected in parallel with a third, identical capacitor. Hence we add the two capacitances to get an equivalent capacitance of 1.50C, or 1.50×24.0 µF = 36.0 µF.



















 



C. C₁ ... C₂

When connected in series the two capacitors have the same charge. By noting that U = ½Q²/C you can see the smaller capacitor C₁ stores the most energy. (Confirm for yourself that if the battery voltage is 6.0 V and C = 10.0 µF, C₁ stores 80 µJ and C₂ stores 40 µJ.)
When connected in parallel the two capacitors have the same voltage. By noting that U = ½CV² you can see the larger capacitor C₂ stores the most energy. (Confirm for yourself that if the battery voltage is 6.0 V and C = 10.0 µF, C₁ stores 180 µJ and C₂ stores 360 µJ.)


















 


C. 6.00 V

The left side of the capacitor is at the higher potential.