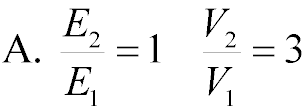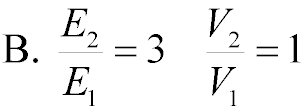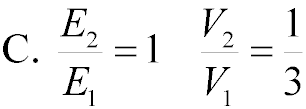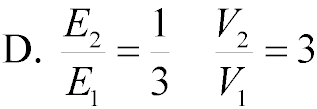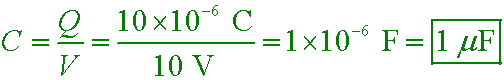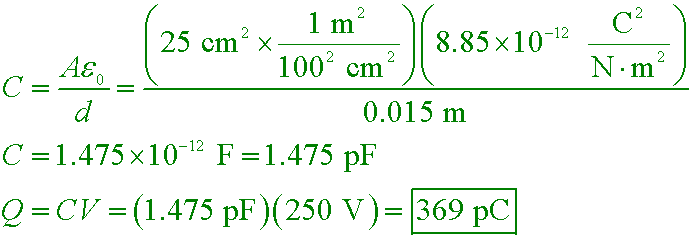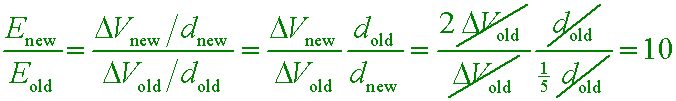Summary

• Electric field & force
• Electric potential energy
• Electric potential
• Point charges

• Quiz Bonus Ch. 19



• Review field and potential

Example #1


• Field and potential inside conductors



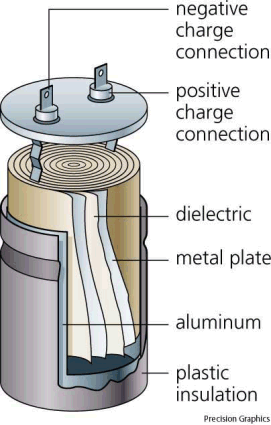
• Capacitance
• definition and applet
• PhET Capacitor Lab
Example #2
Example #3

• energy storage in capacitors
• charge
• potential
• energy storage in fields
Example #4






• Lecture learning outcomes
  A student who masters the topics in this lecture will be able to:
• describe the electric field and the electric potential inside a conductor
• describe the physical features of a capacitor and explain its ability to store charge and energy
• use algebra to find the capacitance C, plate charge Q, or potential difference V when any two of these quantities are given
• use algebra to find the stored energy U, capacitance C, plate charge Q, or the potential difference V when any two of these quantities are given




• Practice:
  Try these additional examples

Example #5

Example #6



• Prepare:
  Read textbook sections 21-1 through 21-2 before the next lecture

gc6 tb16.11
A negatively charged rod is brought near one end of an uncharged metal bar. The end of the metal bar farthest from the charged rod will be charged
A. positive
B. negative
C. neutral
D. none of these
Answer













Knight2 29.CQ.10
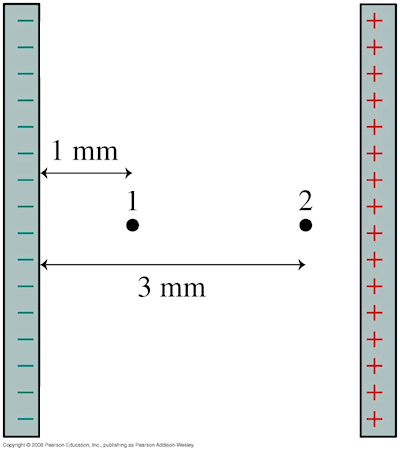
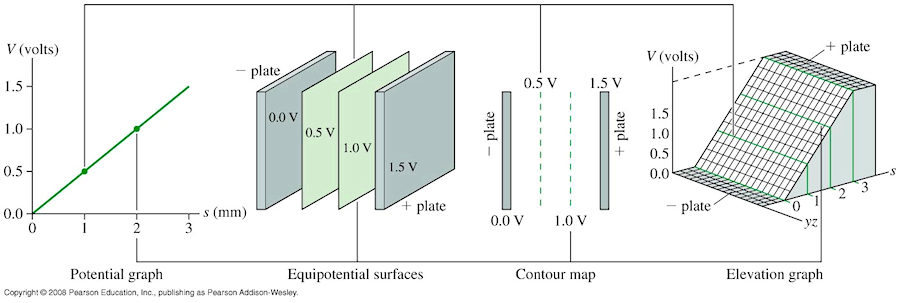
What are the ratios of the fields and potentials at the positions indicated in the figure? Let V = 0 V at the negative plate.







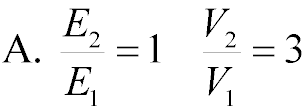
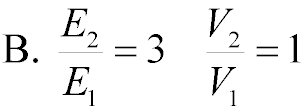
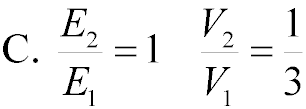
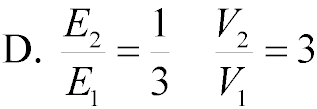
Answer















sj6 26.2
Conductors with charges +10µC and −10µC have a potential difference of 10 V. What is the capacitance?
A. 1 pF
B. 10 pF
C. 1 µF
D. 100 µF
Answer















sj6 26.2b
If the charges are increased by a factor of ten, what will happen to the potential difference?
A. decrease by factor of 100
B. decrease by factor of 10
C. stay the same
D. increase by factor of 10
Answer















gc6 17.50
A capacitor has fixed charges on its plates as the separation between the plates is doubled. What happens to the energy stored in the electric field?
A. U₂ = 4 U₁
B. U₂ = 2 U₁
C. U₂ = 0.5 U₁
D. U₂ = 0.25 U₁
Answer















sb5 26.47
A capacitor with A = 25 cm² and d = 1.5 cm is charged to 250 V. What is the charge on its plates?
A. 151 nC
B. 369 pC
C. 519 µC
D. 17.1 mC
Answer















APB 1998.14
Two parallel conducting plates are connected to a constant voltage source. The magnitude of the electric field between the plates is 2,000 N/C. If the voltage is doubled and the distance between the plates is reduced to 1/5 the original distance, the magnitude of the new electric field is
A. 800 N/C
B. 1,600 N/C
C. 2,400 N/C
D. 5,000 N/C
E. 20,000 N/C
Answer















 



B. negative
The positive charges in the metal bar will be attracted to the negatively charged rod, leaving the opposite end of the bar negatively charged. You can also say that the electrons in the metal bar are repelled by the negatively charged rod.


















 



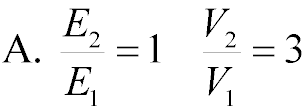
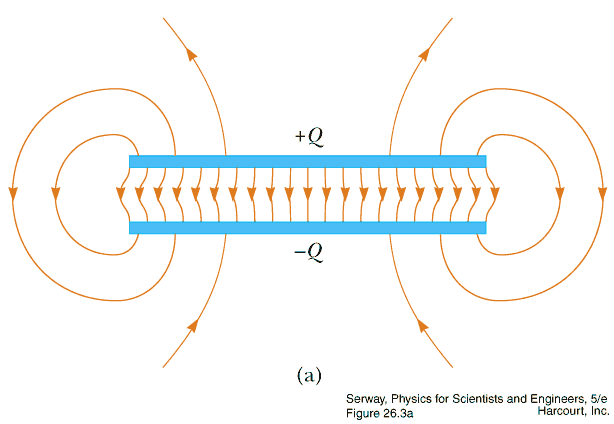
The field is constant in between capacitor plates, but the potential increases linearly.




















 



C. 1 µF





















 



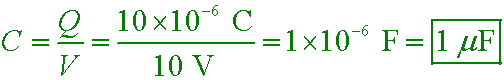
D. increase by factor of 10
The capacitance will remain constant as long as the geometry of the capacitor remains constant. Therefore since C = Q/V the potential difference will increase in linear proportion to the amount of charge.




















 



B. U₂ = 2 U₁
The energy stored in the capacitor is proportional to the charge squared divided by the capacitance, but the capacitance will be cut in half if the plate separation is doubled. Therefore, the energy stored will double. This is because it requires work to pull apart the oppositely charged plates that attract each other.




















 



B. 369 pC





















 



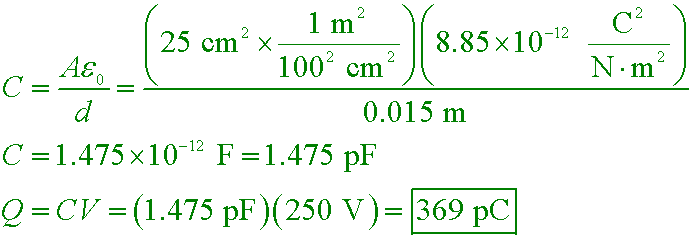
E. 20,000 N/C

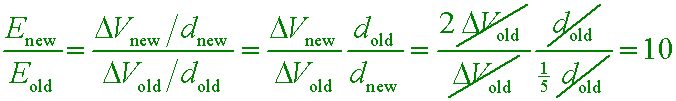
The electric field is uniform and constant between the plates and equals ΔV/d (Eq. 20-4, see also Eq. 20-11). Doubling ΔV will double E, and decreasing d by a factor of 5 will increase E by a factor of 5. The two changes together will increase E by a factor of 10.